№1 из некоторой точки провели l данной плоскости перпендикуляр, равный h ,и наклонная, угол между ними равен 45.найти длину наклонной. №2в основании прямоугольного прямоугольного параллелепипеда лежит квадрат со стороной, равной 2. диагональ параллелепипеда равна 3. найти объем его. №3 ребро куба равно а . найти радиусы шаров: вписанного в куб и описанного около него.

👇

Ответ:

ритуля51

09.06.2022

1. Если из одной точки провели перпендикуляр и наклонную к плоскости, причем угол между ними 45 град., то образовался равнобедренный прямоугольный треугольник, причем длина катета =h, а гипотенуза и есть наклонная, длину которой нужно найти. Воспользуемся теоремой Пифагора:
h^2+h^2=l^2
l=h(2)^1/2
2. Для поиска объема необходимо найти высоту параллелепипеда. Диагональ (по условию =3) является гипотенузой прямоугольного треугольника, катет которого есть диагональ квадрата со стороной =2, по теореме Пифагора это (8)^1/2
Отсюда высота составит (3^2-8)^1/2=1
Определим объем перемножением длин ребер:
2*2*1=4
3. Если ребро куба =а, то диаметр вписанного шара тоже =а, следовательно радиус =а/2
Для описанного шара диагональ куба составляет его диаметр и равна а*(3)^1/2 (находится по теореме Пифагора). Следовательно радиус шара =а/2*(3)^1/2

4,5(52 оценок)

Открыть все ответы

Ответ:

goodsmalgirl

09.06.2022

Пошаговое объяснение:

Посчитаем периметр участка , исключая ворота

20+12+12+16 = 60 клеток - периметр участка , без учета ворот

сторона клетки равна 2 м , значит

60 * 2= 120 м будет длина забора

Поскольку длина 1 листа 4 м , то понадобится

120 : 4 = 30 листов

ответ : 30 листов

Огород , вместе с теплицей занимает площадь

6 клеточек * 4 клеточки = (6*2)*(4*2)= 12*8=96 м²

Площадь теплицы

(1*2)*(5*2)=2*10=20 м²

значит площадь огорода без теплицы

96-20=76 м²

ответ : 76 м²

Наименьшее расстояние от бани до гаража - по прямой , это составит 13 клеточек , значит расстояние будет

13 * 2 = 26 м

ответ : 26 м

4,6(49 оценок)

Ответ:

Маргарита5515

09.06.2022

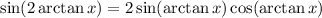$\sin(2\arctan x)=2\sin(\arctan x)\cos(\arctan x)$ . Рассмотрим прямоугольный треугольник со сторонами

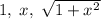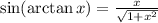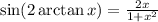$1,\;x,\; \sqrt{1+x^{2}}$ (последняя - гипотенуза). Из него видно, что $\sin(\arctan x)=\frac{x}{\sqrt{1+x^{2}}}$ , а $\cos(\arctan x)=\frac{1}{\sqrt{1+x^2}}$ . Тогда исходный синус перепишется в виде $\sin(2\arctan x)=\frac{2x}{1+x^2}$ .

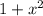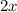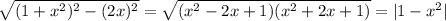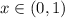Рассмотрим треугольник с гипотенузой $1+x^{2}$ и катетом . Тогда оставшийся катет можно вычислить по теореме Пифагора: $\sqrt{(1+x^{2})^{2}-(2x)^{2}}=\sqrt{(x^{2}-2x+1)(x^{2}+2x+1)}=|1-x^{2}|$ . Пусть рационально и $x\in(0,1)$ . Тогда у треугольника рациональные стороны и синус одного из его углов удовлетворяет требованиям. Теперь достаточно увеличить его стороны в наименьшее общее кратное всех трех знаменателей раз. И требуемый треугольник готов