Посчитаем среднюю скорость в обоих случаях.
Средняя скорость - это всё расстояние AB, деленное на всё время.
1-ый путешественник половину пути AB/2 со скоростью v км/ч пешком, а потом половину пути AB/2 со скоростью w км/ч на автобусе.
Время t1 = AB/(2v)+AB/(2w) = AB/2*(1/v+1/w) = AB/2*(v+w)/(vw) = AB(v+w)/(2vw)
Средняя скорость AB/t1 = 2vw/(v+w)
2 путешественник шел со скоростью v км/ч половину времени t2/2, а потом ехал на автобусе со скоростью w км/ч еще половину времени t2/2.
А всего он
Средняя скорость AB/t2 = (v+w)/2
Чтобы сравнить эти две средние скорость, вычтем 1-ую из 2-ой.
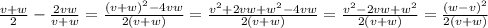
Очевидно, что знаменатель положителен, и числитель тоже положителен при любых w > v.
Значит, у 2-го путешественника средняя скорость больше, и он придет раньше.
1) 4х²+11х-3=(х+3)(4х-1)
2) 5х²-8х+3>0
(5х-3)(х-1)>0
х∈(-∞;3/5)∪(1;+∞)
3) х⁴-5х²-6=0
х²=а
а²-5а-6=0
а1=-1; а2=6
х∉R; x1=-√6; x2=√6
ответ: x1=-√6; x2=√6
4) а12=а1+11d=-5+11×3=-5+33=28
S12=n(a1+an)/2 = 12(-5+28)/2=12×23/2=138
ответ: S12=138
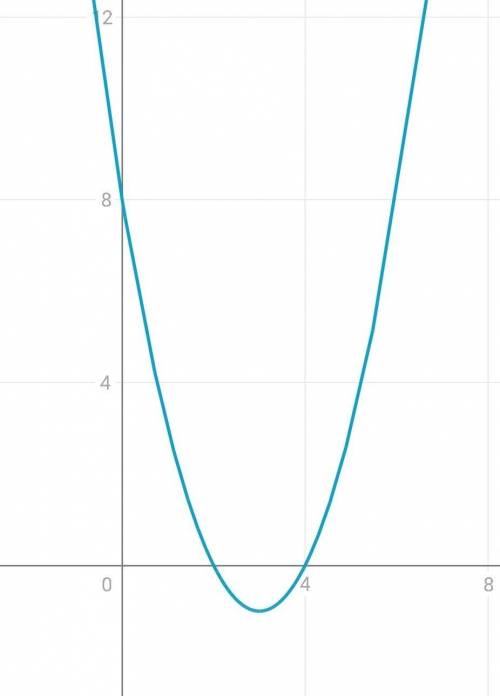
5) у=х²-6х+8
х²-6х+8=0
х1=2; х2=4
у=0²-6×0+8=8
График: парабола, ветки направлены вверх.
С осью Ох пересекается в точках 2 и 4.
С осью Оу пересекается в точке у=8
Ниже приведен график.
6) перевели минуты в часы: 54мин = 0,9ч
х - скорость первой группы
у - скорость второй группы
18=2×(x+y) => x+y=9
Составим систему:
{х+у=9
{18/х - 18/у = 0,9
Упростим второе уравнение, а из первого вытащим х:
{х=9-у
{18у-18х=0,9ху
Подставим значение Х во второе уравнение:
18у-18(9-у)=0,9у(9-у)
18у-162+18у-8,1у+0,9у²=0
0,9у²+27,9у-162=0 |:0,9
у²+31у-180=0
по т.Виета: у= -36 – посторонний корень; у=5
х=9-5=4
ответ: Скорость первой группы 4км/ч; скорость второй группы 5км/ч