1) 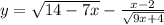
Область определения этой функции должна удовлетворять двум условиям:
1) подкоренное выражение неотрицательно (т.е. 14 - 7х ≥ 0 и 9х + 4 ≥ 0)
2) знаменатель дроби отличен от нуля (т.е.  )
)
Поэтому эти условия удобно записать в виде системы:

Решением системы неравенств будет множество, которое и есть область определения функции.
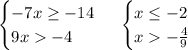
![x\in(-\frac{4}{9};\ 2]](/tpl/images/0525/6406/397dd.png)
ответ: ![(-\frac{4}{9};\ 2]](/tpl/images/0525/6406/39742.png)
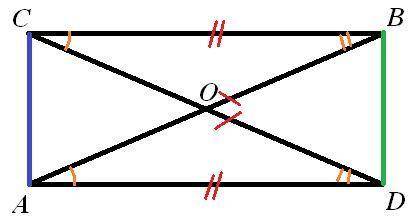
2) Рисунок к задаче - во вложении.
Проведем отрезки BD и AC.
Получим, что ΔABD=ΔCDB по трем сторонам (BD-общая, CB=AD, CD=AB) и ΔCDA=ΔABC по трем сторонам (AC-общая, CB=AD, CD=AB).
Из равенства ΔABD и ΔCDB следует, что соответственно равны ∠A и ∠C.
А из равенства ΔCDA и ΔABC следует, что соответственно равны ∠D и ∠B.
Наконец, рассмотрим ΔCOB и ΔAOD. У них CB=AD, ∠A=∠C, ∠В=∠D. Значит, ΔCOB = ΔAOD по стороне и прилежащим к ней углам.
Из равенства ΔCOB и ΔAOD следует равенство соответственных сторон СО и AO.
Доказано.

автобуса - a km/h
скорость грузовика будет - g km/h
расстояние - s km
ну и время t1 - сколько ехал часо грузовик, t2 - время общего движения
тогда:
нам известно, что по какой-то причине, автобус выехал на 2 часа позже грузовика, значит грузовик уже был от него не расстоянии:
а*t1
как всем, даже маленьким, известно что скорость двух объектов движущихся в разные стороны, равна сумме этих скоростей:
(а+g)
а если ещё всё это дело умножить на время, то узнаем на сколько км они уедут друг от друга:
(a+g)*t2=s km
а теперь к этому прибавить то, что проехал грузовик... вот мы и получим формулу:
(a*t1)+(a+g)*t2=s
ну а так, как нам известно s=416 km, a=72km/h, g=68km/h t1=2 ч... то найти t2 проще пареной репы:
(68*2)+(72+68)t2=416
136+140t2=416
140t2=416-136
140t2=280
t2=2
ответ: после выезда автобуса на расстоянии 416 км они будут чере 2 часа.
Пошаговое объяснение:
9x-2x=42
7x=42
x=6 => 1 часть равна 6
1 число = 2*6=12
2 число =5*6 = 30
3 число = 9*6=54.
54+30+12=96