В задании представлены дроби, имеющие одинаковый числитель.
Сравниваются по правилу сравнения дробей с одинаковым числителем: "Из 2-х дробей с одинаковым числителем больше та дробь, у которой знаменатель меньше". иными словами, дробь - это деление, если 2 делим на 1, то 2/1=2. Если 2 делим на 2, то 2/2=1.
1) 1/5 и 1/3, 5>3 => 1/5<1/3
2) 1/7 и 1/9, 7<9 => 1/7>1/9
3) 2/13 и 2/3, 13>3 => 2/13<2/3
4) 4/5 и 4/7, 5<7 => 4/5>4/7
5) 11/13 и 11/15, 13<15 => 11/13>11/15
6) 8/15 и 8/11, 15>11 => 8/15<8/11
Пошаговое объяснение:
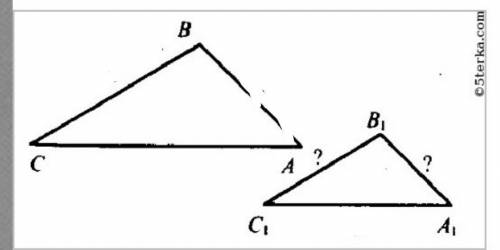
1 задача.
Треугольник ABC и A1B1C1 подобны, следовательно;
AB/A1B1=AC/A1C1=BC/B1C1
Возьмём большую сторону A1C1.
Значит выходит:
10/A1B1=15/12=12/B1C1 отсюда:
A1B1=10*12/15=8;B1C1=12*12/15=9.6
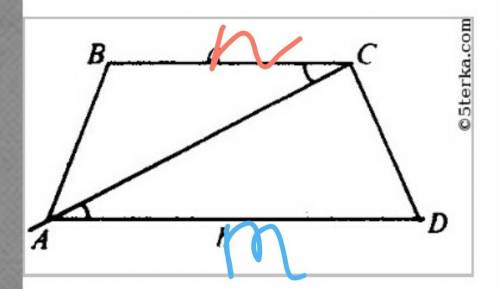
2 задача.
Треугольники ABC и ACD подобны;AD=m и BC=n.
Два треугольника подобны значит:AB/DC=BC/AC=AC/AD
AC²=AD*BC(свойства пропорции)
т.е. АС²=m*n
3 задача.
прямая пересекающия стороны в точках M и N
В треугольнике ABC и MNC;угол С общий.
угол М=угол А(потому что АВ||a)
Значит треугольник АВС и МNC подобны (по двух углам),отсюда:
BC/NC=AB/MN=AC/MC=4+5/5
Вот что выходит:AB/MN=9/5;BC/NC=9/5;AC/MC=9/5
MN=5/9AB=1.4×5=7см
NC=5/9BC=2×5=10см
MC=5/9AC=1.7×5=8.5см