ответ: min y = -3, max y = -1.
Пошаговое объяснение:
Находим производную.
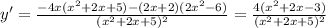
Приравниваем нулю множитель числителя с переменной.
Решаем уравнение x^2+2*x-3=0.
Ищем дискриминант:
D=2^2-4*1*(-3)=4-4*(-3)=4-(-4*3)=4-(-12)=4+12=16;
Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(√16-2)/(2*1)=(4-2)/2=2/2=1;
x_2=(-√16-2)/(2*1)=(-4-2)/2=-6/2=-3.
Находим знаки производной в промежутках между критическими точками.
x = -4 -3 0 1 2
y' = -0,118343 0 0,48 0 -0,118343 .
Как видим, в точке х = -3 минимум функции, а в точке х = 1 - максимум.
Находим значения функции в этих точках.
у(-3) = (-2(9+3))/(9-6+5) = -24/8 = -3.
у(1) = (-2(1+3))/(1+2+5) = -8/8 = -1.
На заданном промежутке [-5; 1] значение функции у(1) = -1 является максимальным, а у(-3) =-3 минимальным.
Исследовать функцию f (x) = 4x³–6x² и построить ее график.
1. Область определения функции - вся числовая ось.
2. Функция f (x) = 4x³–6x² непрерывна на всей области определения. Точек разрыва нет.
3. Четность, нечетность, периодичность:
График четной функции симметричен относительно оси ОУ, а нечетной — относительно начала координат О.
f(–x) = 4(–x)³–6(–x)² = –(4x³+6x²) ≠ –f(x),
f(–x) = 4(–x)³3–6(–x)² = –(4x³+6x²) ≠ –f(x)
Функция не является ни четной, ни нечетной. Функция непериодическая.
4. Точки пересечения с осями координат:
Ox: y=0, 4x³–6x²=0, 2x²(2x–3)=0 ⇒ x=0, x=3/2. Значит (0;3/2), - точки пересечения с осью Ox.
Oy: x = 0 ⇒ y = 0. Значит (0;0) - точка пересечения с осью Oy.
5. Промежутки монотонности и точки экстремума:
y'=0 ⇒ 12x²–12x =0 ⇒ 12x(x–1) = 0 ⇒ x = 0, x = 1 - критические точки.
Если производная положительна - функция возрастает, если производная отрицательна - функция убывает:
отрезок -∞ < x < 0 функция возрастает,
отрезок 0 < x < 3/2 функция убывает,
отрезок 3/2 < X < ∞ функция возрастает.
7*. Вычисление второй производной: у =4x³–6x²,
f '(x) = 12x² - 12x. f ''(x) = 24x - 12.
y''=0, 24x–12= 0, x = 12/24 = 1/2.
8*. Промежутки выпуклости и точки перегиба:
отрезок -∞ < x < 1/2 график функции выпуклый вверх,
точка перегиба х = 1/2,
отрезок 1/2< x < ∞ график функции выпуклый вниз.
9. Найдем значение функции в дополнительной точке: f(1/2) = 4*(1/2)³– 6(1/2)² = 4/8 -6/4 = (4-12) / 8 = -8/8 = –1.
10. Искомый график функции в приложении
2)435098