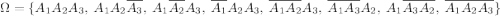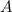Записать: 1) наименьшее шестизначное число; 2) наибольшее шестизначное число; 3) наибольшее семизначное - id424497520230607 от vitalytubvitalnru 07.06.2023 05:13

Question

Математика: Записать: 1) наименьшее шестизначное число; 2) наибольшее шестизначное число; 3) наибольшее семизначное число; 4) наименьшее семизначное число. ! булу если по можете!

vitalytubvitalnru · Accepted Answer

Пусть

- событие, состоящее в том, что мишень будет поражена два раза.
Событие A_1

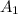- {попадание во время первого выстрела}
Событие A_2

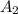- {попадание во время второго выстрела}
Событие A_3

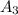- {попадание во время третьего выстрела}

Событие

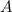можно представить в виде суммы трех несовместных событий: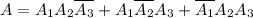 $A=A_1A_2\overline{A_3}+A_1\overline{A_2}A_3+\overline{A_1}A_2A_3$

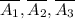где $\overline{A_1},\overline{A_2},\overline{A_3}$ - противоположные события соответственно при первом, втором и третьем выстрелах, а каждое из слагаемых является произведение трех независимых событий.

Множество $\Omega$ всех возможных взаимоисключающих исходов данного опыта (испытания, эксперимента) называется пространством элементарных событий

$\Omega=\{A_1A_2A_3,~A_1A_2\overline{A_3},~A_1\overline{A_2}A_3,~\overline{A_1}A_2A_3,~\overline{A_1A_2}A_3,~\overline{A_1A_3}A_2,~A_1\overline{A_3A_2},~\overline{A_1A_2A_3}\}$

Записать: 1) наименьшее шестизначное число; 2) наибольшее шестизначное число; 3) наибольшее семизначное число; 4) наименьшее семизначное число. ! булу если по можете!

MOGZ ответил