а) 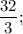 б) 2; в)
б) 2; в) 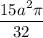
Пошаговое объяснение:
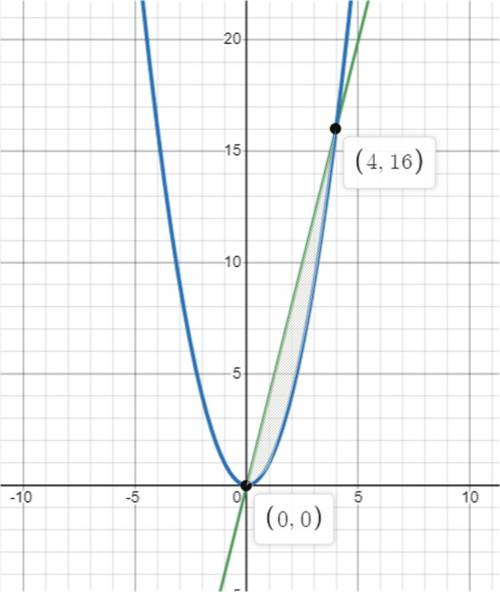
а) Найдем точки пересечения указанных графиков 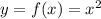 и
и 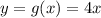 (рис. 1), приравняв правые части:
(рис. 1), приравняв правые части:
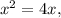
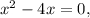
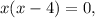
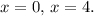
Так как на промежутке ![[0;\,\,4]](/tpl/images/4978/6389/04e4e.png)
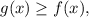 то применяя формулу Ньютона-Лейбница, получаем
то применяя формулу Ньютона-Лейбница, получаем
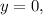
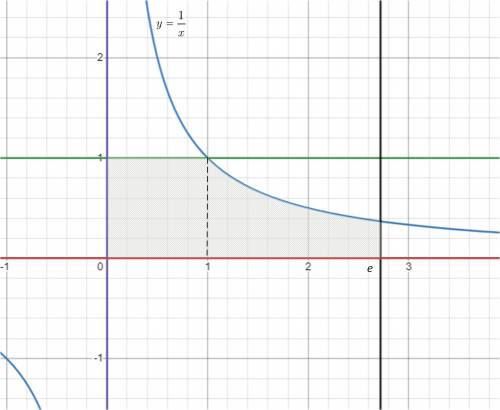
б) Нарисуем в одной координатной плоскости все указанные линии и заштрихуем область, площадь которой необходимо найти. Разобьем получившуюся фигуру на две части прямой 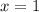 (рис. 2).
(рис. 2).
Тогда левая часть фигуры — квадрат со стороной 1, его площадь равна 1.
Площадь правой части фигуры найдем как площадь криволинейной трапеции, ограниченной графиком функции 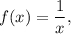 прямыми
прямыми 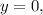
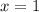 и
и 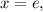 используя формулу Ньютона-Лейбница:
используя формулу Ньютона-Лейбница:
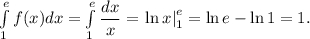
Таким образом, площадь заданной фигуры равна 1 + 1 = 2.
в)
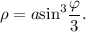
(рис. 3 для случая 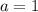 ).
).
Решаем неравенство
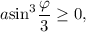
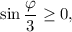
![\displaystyle\frac{\varphi }{3} \in [\pi k;\,\,\pi + \pi k],\\](/tpl/images/4978/6389/95d76.png)
![\varphi \in [3\pi k;\,\,3\pi + 3\pi k].](/tpl/images/4978/6389/60642.png)
Для вычисления площади криволинейного сектора воспользуемся формулой
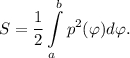
Из формулы синуса тройного угла следует, что
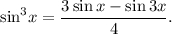
Тогда
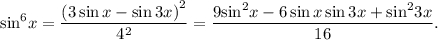
Понижая степень синуса и записывая произведение синусов в виде суммы, получим
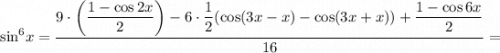
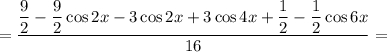
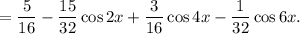
Тогда площадь
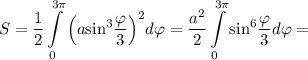
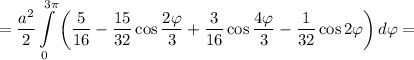
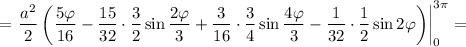
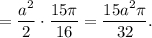
Объяснение:
Дано: пусть ∆АВС, АВ = ВС = 8см, АС = 12см
Найти: DO - ?
⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀Решение Это ромб. Стороны попарно параллельны и диагонали перпендикулярны и точкой пересечения делятся пополам. DО=ОВ. AO=OC=6см∆АВО - прямоугольный. Найдем Катет (ВО) применив теорему Пифагора. Она гласит, что квадрат гипотенузы равен сумме квадратов катетов.⠀⠀⠀⠀AB²=BO² + AO²
⠀⠀⠀⠀8² = ВО² + 6²
Отсюда выразим катет ВО.⠀⠀⠀⠀ВО² = 8² - 6²
⠀⠀⠀⠀ВО² = 64 - 36
⠀⠀⠀⠀ВО² = 28
Извлечем корень.⠀⠀⠀⠀ВО = √28
⠀⠀⠀⠀ВО = 2√7(см)
Т.к. ВО = DO, то ответ 2√7(см)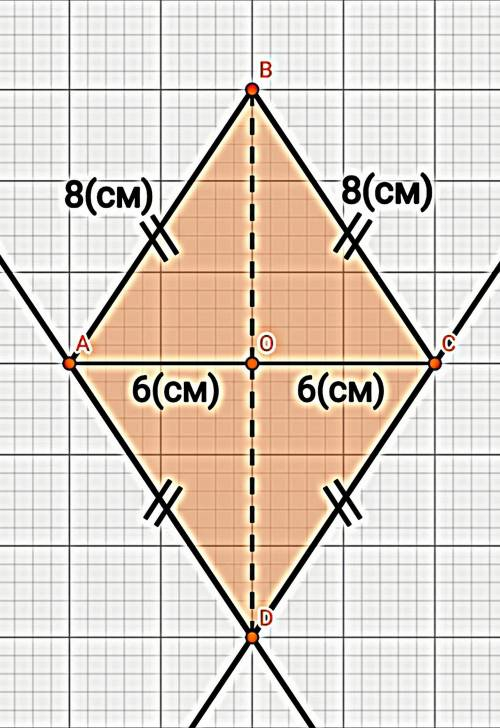
Различают торцевой разрез, перпендикулярный продольной оси ствола (см. рисунок), радиальный разрез, перпендикулярный торцевому разрезу и проходящий через сердцевину ствола; тангентальный разрез, проходящий по касательной к годовым слоям на некотором расстоянии от сердцевины.
Строение и свойства древесины неодинаковы по различным разрезам. На поперечном разрезе ствола различают кору, ее пробковый и лубяной слои, камбий; видна древесина, ее заболонь и ядро, где различны годовые слои, сердцевинные лучи и сердцевина
Сердцевина расположена в центре ствола дерева по всей его длине. Она имеет рыхлое строение, непрочна и подвержена быстрому загниванию. У хвойных пород диаметр сердцевины равен 3-4 см, а у лиственных несколько больше. Ежегодно прирост древесины происходит на одно годовое кольцо, образуемое камбием под корой.
При росте дерева древесина сердцевины разрушается, поэтому диаметр ее по направлению к кроне постепенно увеличивается. У некоторых пород, например сосны, лиственницы, дуба, ясеня и кедра, часть древесины, расположенная ближе к сердцевине, имеет более темную окраску и пониженную влажность. Эту наиболее ценную часть древесины называют ядром, а остальную часть, расположенную в сторону коры, - заболонью. Существуют породы, у которых отсутствует ядро, у них одинаковый цвет древесины по всему сечению.
Древесина ядра отличается прочностью, плотностью и твердостью, а также большой сопротивляемостью к загниванию, чем заболонь, которая состоит из молодых клеток, отличающихся меньшей плотностью древесины. Сокодвижение - перемещение воды с растворенными в ней питательными веществами - происходит по заболони. Толщина заболони зависит от породы дерева, его возраста и условий роста. Рост ядра с отмиранием клеток заболони превращается в древесину ядра.
У березы, бука, клена, осины и ольхи центр ствола имеет темную окраску, свидетельствующую о начальной стадии загнивания. Эту часть ствола называют ложным ядром.
Между заболонью и корой располагается тонкий слой живых клеток - камбий. В вегетационный период деление камбиальных клеток образует новые клетки древесины и коры. При этом дерево растет как в толщину, так и в длину. Кора состоит из наружного пробкового слоя и внутреннего лубяного.
Наружный слой защищает дерево от атмосферных влияний и механических повреждений, внутренний передает вниз по стволу органические питательные вещества, выработанные в листьях кроны.
У большинства хвойных пород в поперечном разрезе ствола различны годовые слои в виде концентрических окружностей. Ежегодно при нормальном росте образуется один годовой слой. Его толщина (в направлении радиуса) у разных древесных пород различна. Ранняя древесина годового слоя сердцевины отличается от поздней древесины, находящейся ближе к коре. Это объясняется ростом ранней древесины годового слоя весной и в начале лета. В это время в почве мало влаги и клетки ранней древесины рыхлые и светлые, обеспечивающие сокодвижение. Поздняя древесина годового слоя растет в конце лета и осенью.
У лиственных пород клетки поздней древесины (годового слоя) состоят из опорных тканей, а у хвойных пород - из толстостенных трахеид, более темных по цвету и отличающихся плотностью и прочностью.
Ширина годовых слоев зависит от возраста дерева, от породы и условий роста. У молодых деревьев годовые слои обычно более широкие, кроме ивы, имеющей только узкие годовые слои. У сосны, растущей на севере, годовые слои более узкие, чем у сосны, растущей в южных широтах. Свойства древесины характеризует ширина годовых слоев. Хвойные породы с узкими годовыми слоями отличаются большей прочностью и смолистостью.
Сосна с узкими годовыми слоями краснобурого цвета более ценна, чем с широкими годовыми слоями. Древесина хвойных пород, на торцевом разрезе которой в радиальном направлении в 1 см насчитывается не менее трех и не более 25 годичных слоев, считается лучшей. У лиственных древесных пород наоборот, чем шире годовые слои, тем плотнее, тверже и более прочная древесина. Это характерно для дуба, каштана, ильма, ясеня, вяза. У этих пород в весенний период независимо от климатических, почвенных и других условий образуется 2-3 ряда крупной проводящей ткани (трахеид), а затем - поздняя древесина годового слоя, состоящая из механически прочных тканей.
Сердцевинные лучи располагаются в стволе в радиальном направлении. Различают первичные и вторичные лучи. Первичные сердцевинные лучи начинаются от сердцевины и доходят до коры, вторичные начинаются недалеко от сердцевины и продолжаются до коры. По сердцевинным лучам в горизонтальном направлении перемещаются вода, питательные вещества и воздух.