Пошаговое объяснение:
Это задача на теорему Байеса. Гипотезы:
Н1 -- взята винтовка с оптическим прицелом. Вероятность гипотезы Р (Н1) = 4/10 = 0.4.
Н2 -- взята винтовка без оптического прицела. Вероятность гипотезы Р (Н2) = 6/10 = 0.6.
Событие А -- попадание в цель. Условные вероятности попадания для каждой из гипотез: Р (А | H1) = 0.95, Р (А | H2) = 0.8.
Полная вероятность попадания: Р (А) = Р (А | H1) * Р (Н1) + Р (А | H2) * Р (Н2) = 0.4*0.95 + 0.6*0.8 = 0.86.
Апостериорная вероятность первой гипотезы при условии, что пуля попала в мишень:
P(H1 | A) = P(A | H1) * P(H1) / P(A) = 0.4*0.95/0.86.
Апостериорная вероятность второй гипотезы при условии, что пуля попала в мишень:
P(H2 | A) = P(A | H2) * P(H2) / P(A) = 0.6*0.8/0.86.
Отсюда P(H2 | A) > P(H1 | A), то есть более вероятно, что стрелок стрелял из винтовки без оптического прицела.
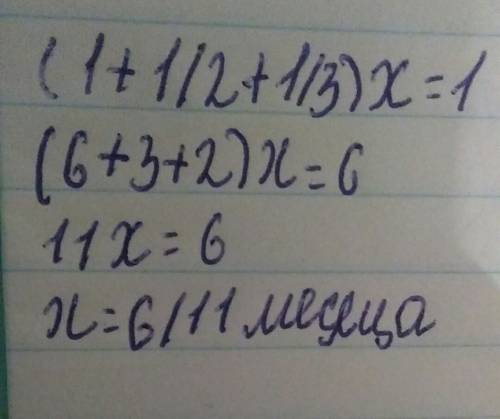
Нужно показать, что не менее 3 тыс. чисел превратятся в 0.
1) После первой операции в 0 превратится любое число, у которого есть 0 в написании.
Кол-во чисел с 0 на втором месте:
- на первом месте любая из 9 цифр, на третьем месте - любая из 10, на 4-ом - любая из 10, всего 9*10*10=900.
- с 0 на третьем месте (но не 0 на втором - они учтены в предыдущем случае):
9*9*10=810.
- с 0 на 4-ом месте, но не на 2-ом и 3-ем:
9*9*9=729.
Всего с 0-м в написании: 900+810+729=2439.
2) После первой операции 0 появится у всех чисел, в написании которых есть 5-ка и хотя бы одна из четных цифр: 2,4,6,8.
Пусть 5-ка на первом месте, на втором - одна из 2,4,6,8, на третьем и 4-ом - любые цифры, кроме 0. Таких чисел 4*9*9=324
Если 5-ка на втором месте, на первом - любая из 2,4,6,8, на третьем и 4-ом - любые цифры, кроме 0. Таких чисел также 324.
Итого, мы нашли 2439+324+324 =3087 различных 4-х значных чисел, которые превратятся в 0. Ч.т.д.