1) 3/7 + 5/14 = 6/14 + 5/14 = 11/14
2) 2 1/8 + 3 5/12 = 2 3/24 + 3 10/24 = 5 13/24
3) 6 15/21 + 2 9/14 = 6 30/42 + 2 27/42 = 8 57/42 = 9 15/42 = 9 5/14
4) 5 13/15 + 1 7/12 = 5 52/60 + 1 35/60 = 6 87/60 = 7 27/60 = 7 9/20
5) 1 - 9/11 = 11/11 - 9/11 = 2/11
6) 8/9 - 7/12 = 32/36 - 21/36 = 11/36
7) 8 - 5 4/9 = 7 9/9 - 5 4/9 = 2 5/9
8) 7 3/8 - 3 5/6 = 7 9/24 - 3 20/24 = 6 33/24 - 3 20/24 = 3 13/24 = 3 13/24
9) 3/8 * 2/9 = 6/72 = 1/12
10) 2 1/10 * 1 1/14 = 21/10 * 15/14 = 9/4 = 2 1/4
11) 3 2/5 * 1/19 = 17/5 * 1/19 = 17/95
12) 5/7 : 3/8 = 5/7 * 8/3 = 40/21 = 1 19/21
13) 4 4/9 : 2 2/3 = 40/9 : 8/3 = 40/9 * 3/8 = 5/3 = 1 2/3
Пошаговое объяснение:
уже решала на этом ресурсе, но повторю еще разик....
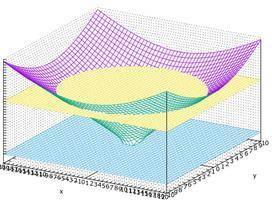
1 формула - это однополостный гиперболоид
две других - это плоскости
объем тела, содержащегося между плоскостями z = а и z = Ь, выражается формулой:
, где S (z) — площадь сечения тела плоскостью, перпендикулярной к оси ординат в точке z.
плоскость, перпендикулярная оси Оz, в точке с аппликатой z пересекает гиперболоид по эллипсу
площадь эллипса через полуоси
S= πab
запишем наш эллипс
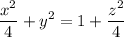
теперь каноническое уравнение эллипса
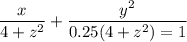
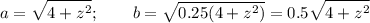
тогда площадь будет
S(z) = πab = π*0.5
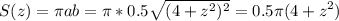
и тогда объем
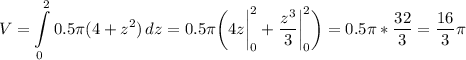
2.6:3=0.86 вероятность сдать все экзамены.