Пошаговое объяснение:
Дано трехзначное число abc, где а- число сотен , b- число десятков , с - число единиц. При этом b=c. Получаем уравнение
a+b+b=12
a+2b=12
Если в числе(100a+10b+b ( c=b) поменять местами первую и вторую цифры , получим число 100b+10a+b . Составим уравнение
(100b+10a+b)-(100a+10b+b)= 270
101b+10a-100a-11b=270
90b-90a=270
разделим на 90
b-a=3
Получаем систему уравнений :
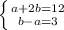
из второго уравнения
b=3+a
подставим в первое уравнение
а+2(3+а)=12
а+6+2а=12
3а=6
а=2
b=3+2=5
Искомое число 255
Проверка :
2+5+5=12
525-255= 270
270=270
sin4x - cos4x=sin2x - 1/2
1. Формула квадрата суммы (sin2x + cos2х)2 = sin4x + 2sin2xcos2х + cos4x
Поэтому sin4x + cos4x = sin4x + 2sin2xcos2х + cos4x - 2sin2xcos2х
2. Получается равенство
(sin2x + cos2х)2 - 2sin2xcos2х = sin2x - 1/2
3. sin2x + cos2х = 1, поэтому выражение приобретает вид
12 - 2sin2xcos2х = sin2x - 1/2
4. 2sin2xcos2х = 1/2 sin22x
Получается выражение
1 - 1/2 sin22x = sin2x - 1/2
Переносим все в левую часть
1 - 1/2 sin22x - sin2x + 1/2 = 0
- 1/2 sin22x - sin2x + 3/2 = 0 | * (-2)
sin22x + 2sin2x - 3 = 0
5. Пусть sin2x = а
а2 + 2а - 3 = 0
Решаем квадратное уравнение.
D = 4 + 12 = 16 (кв.корень равен 4)
а1 = (- 2 + 4)/2 = 1
а2 = (- 2 - 4)/2 = - 3
6. Возвращаемся к замене sin2x = а
sin2x = - 3 (не может быть, синус всегда больше - 1, но меньше 1)
sin2x = 1
2х = П/2 + 2Пn
x = П/4 + Пn, n - целое число.