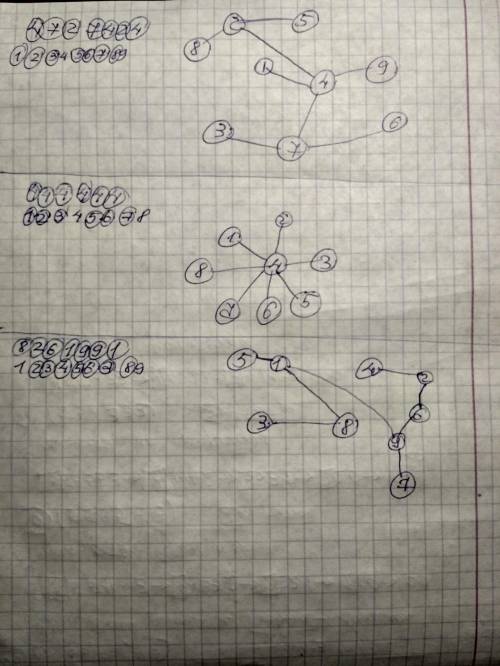
Задание 1
ответ в приложении
Задание 2
Тут, очевидно, опечатка, k<n. В дереве на n вершинах не может быть вершины степени n.
n=1:
k=0 - одно дерево, состоящее из одной вершины.n=2:
k=0 => граф не связный => не деревоk=1 => одно дерево, состоящее из одного ребраn>2:
k=0 => граф не связный => не деревоk>0 => Тогда каждому дереву поставим в соответствие код Прюфера. Его длина - n-2. Т.к. вершина 1 имеет степень k, то встречается в нем k-1 раз. Тогда для остальных n-1 вершин остается n-2-(k-1)=n-k-1 мест. Тогда всего таких кодов Прюфера, и, следовательно, деревьев,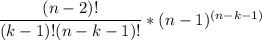
Задание 3
Найти количество деревьев с n вершинами, имеющими вершину степени n-2.
Зафиксируем номер этой вершины. Тогда в коде Прюфера она встречается n-3 раз. Тогда для остальных n-1 вершин остается n-2-(n-3)=1 место. Кол-во выбора номера вершины степени n-2 из n равно n. Тогда искомое число деревьев равно 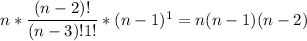
Перевод: классифицируйте эти числа на простые множители.
На математическом языке разложите.
2139 I 3 2139=3*23*31
713 I 23
31 I 31
1
1085 I 5 1085=5*7*31
217 I 7
31 I 31
3751 I 11 3751=11*11*31
341 I 11
31 I 31
4805 I 5 4805=5*31*31
961 I 31
31 I 31
1225 I 5 1225=5*5*7*7
245 I 5
49 I 7
7 I 7
961 I 31 961=31*31
31 I 31
11 495 I 5 11495=5*11*11*19
2299 I 11
209 I 11
19 I 19
19 855 I 5 19855=5*11*19*19
3971 I 11
361 I 19
19 I 19
47 096 I 7 47 096=2*2*2*7*29*29
6728 I 2
3364 I 2
1682 I 2
841 I 29
29 I 29
1914 I 2 1914=2*3*11*29
957 I 3
319 I 11
29 I 29
399 I 3 399=3*7*19
133 I 7
19 I 19
7163 I 13 7163=13*19*29
551 I 19
29 I 29
ВСЕ!