ответ: Пустое множество!
Пошаговое объяснение:
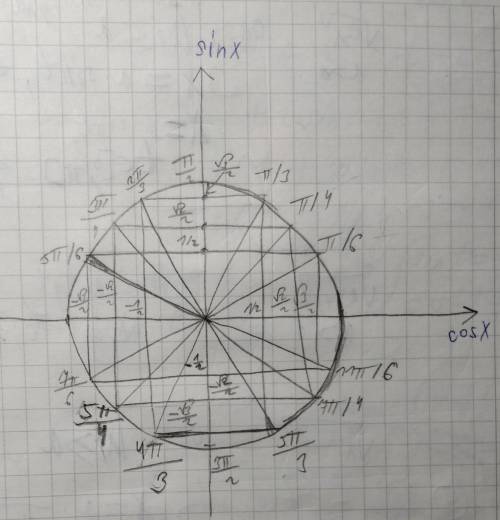
Графически (а в более сложных случаях и методом интервалов, но не в данной задаче) неравенства с тригонометрическими функциями решать как по мне наиболее удобный вариант – нужно только знать какие значения и где на окружности, если что я прикрепила свой может неаккуратный, но применимый для решения рисунок со значениями. Если что, синус угла x – ордината точки, что получена поворотом точки с координатами 1;0 вокруг начала координат на направленный угол x (направленный угол значит двигается против часовой стрелки положительный угол и по угол со знаком –)
А косинус угла х абсцисса точки, полученная аналогичным образом.
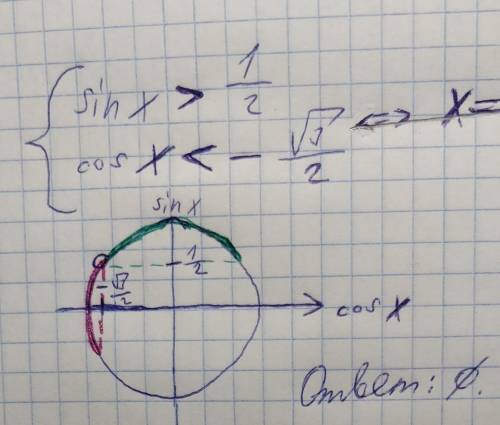
В этой задаче рисуем и получается, что единственное возможное пересечение (а так как у нас система, это и будет решением) – значение угла, чей синус равен 1/2, а косинус –√3/2, НО так как тут в системе строгие неравенства, то ответом является пустое множество.
Пусть х- длина отрезка АВ
у- длина отрезка CD
Зная, что по сусловию задачи отрезок AB на 2 см больше отртезка CD, составляем первое уравнение системы:
x-2=y
Зная, что по условию задачи если длину отрезка АВ увеличить на 10 см, адлину отрезка CD увеличить в 3 раза, то получатся равные результаты, состоюляем второе уравнение ситемы:
х+10=3у
Составляем систему уравнениеавнений
{х-2=у
{х+10=3у
{х-2=у
{х+10=3у|(-1)
{х-у=2
+
{-х+3у=10
2у=12
у=6
х-2=у
х-2=6
х=8 (AB)
Проверка:
Если далина отрезка АВ= 8, CD=6, то АВ больше отрезока CD на 8-6=2, что соответствует условию заддачи.
ответ: AB= 8 см
113*3=339 (мы одну треть умножаем на 3)