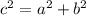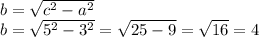)
. Но мы помним, что найденная нами длина катета прямоугольного треугольника (4 см) составляет лишь половину большей диагонали ромба. Следовательно вся большая диагональ ромба будет равна 2*4=8 см.
дано; Пправильная Δ пирамида
а-сторона основания, b-апофема
объем пирамиды равен V=1/3* Sоснования* h (синяя)
Sоснов= 1/2 а*DC
BP ΔADC прямоугольный, ∠АДС=30 АС=1/2а
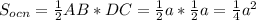
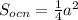
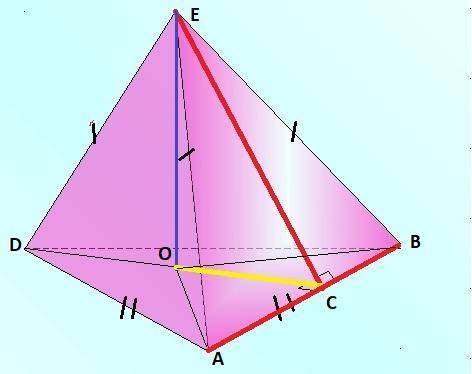
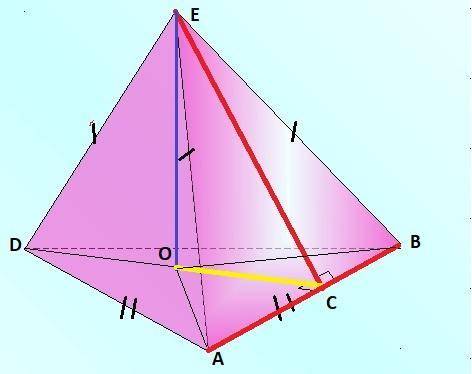
из Δ основания (Δравносторонний), из вершины(A и B) проведем отрезки, соединяющие точку пересечения высоты пирамиды(синяя) с плоскостью основания(O), в полученном ΔAOC прямоугольный ∠OAC=30° ⇒ ОC=1/2*AB=a
из Δ на боковой грани, равнобедренный из ΔEOC прямоугольный,
по т.Пифагора находим ЕО = √b²-(a/2)²
подставляем в формулу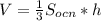 
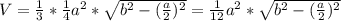
4х машин на второй стоянке
х+ 12 машин стало на первой стоянке
4х - 12 машин стало на второй стоянке
х + 12 = 4х - 12
12 + 12 = 4х - х
4х - х = 24
3х = 24
х = 24 : 3
х = 8 машин - было на первой стоянке
4 * 8 = 32 машины - было на второй стоянке
ответ: 8 машин, 32 машины.
проверка: 32 : 8 = 4 раза, 8 + 12 = 32 - 12, 20 = 20.