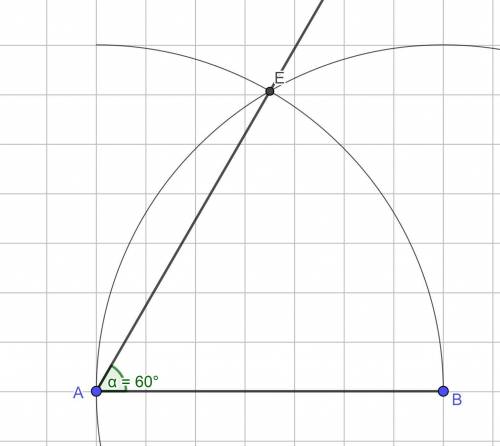
1) Строим угол в 60°. Для этого из концов произвольного отрезка, как из центров проводим окружности радиусом равным длине этого отрезка. Соединяем одну из точек их (окружностей) пересечения с концами отрезка - получаем равносторонний треугольник, то есть угол в 60° - построили! (см. рисунок 1, окружности с центром A, B и радиусами AB пересекаются в точке E)
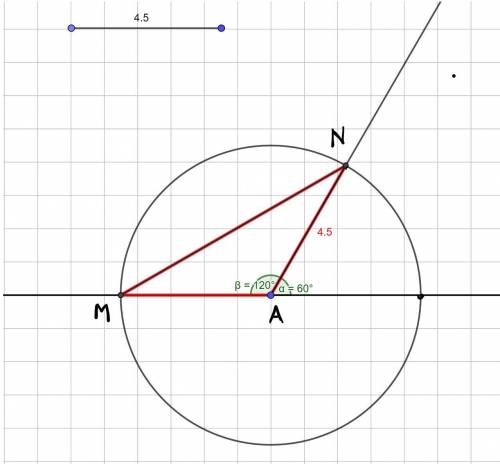
2) Строим угол, смежный построенному в 1), продлив одну из его сторон за вершину. Получаем угол в 180° - 60° = 120°
3) Откладываем на сторонах угла из 2) отрезки длиной 4 см 5 мм
4) Получившиеся точки соединяем (на рисунке 2 точки M, N!)
1) Установим с линейки расстояние между ножками циркуля 4 см 5 мм = 4,5 см;
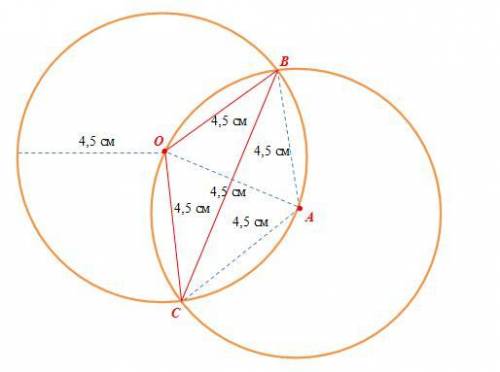
2) Отметим на бумаге произвольную точку и обозначим через О (см. рисунок);
3) Проводим окружность с центром в точке О радиуса 4,5 см;
4) Выберем любую точку окружности, например, точку А и проводим окружность с центром в точке А радиуса 4,5 см;
5) Точки при пересечении окружностей обозначим В и С;
6) Точку О соединим с точками В и С с линейки отрезками;
7) Соединим отрезком с линейки точки В и С.
Построенный треугольник ОВС является решением задачи.
Докажем это:
а) Длины отрезков ОВ и ОС равны 4,5 см как длина радиуса окружности;
б) Так как длины отрезков ОВ, ОС, ОА, ВА, СА равны длине радиуса, то треугольники ОВА и ОСА равносторонние. У равносторонних треугольников все углы равны 60°. Тогда ∠ВОА=60° и ∠СОА=60°, откуда ∠СОВ=∠ВОА+∠СОА=120°.
Что и требовалось.
2)−3 · (72 − 138)=-3* (-66) =198
3) 4 · (43 − 150)=4*(-107) =-428
4) 6 · (25 − 131)=6* (-106) =-636
5) (31 − 12) · (32 − 62)=19* (-30) =-570
6) (13 − 44) · (27 − 47)=-31* (-20) =620
7) (39 − 57) : (27 − 18)=-18:9=-2
8) (63 − 84) : (14 − 21)=-21: (-7) =3
9) −2 · (11 − 36)=-2* (-25) =50
10) 5 · (74 − 93)=5* (-19) =-95
—————————
Удачи!!
—————————