1) 3 5/14 * 7/9 - 2 3/14 * 7/9 2) 7 1/5 * 2 1/8+7 1/5 * 1/58 3) 3/4 * 1 3/5+1 3/5 * 1 3/8 - 1 1/2 * 1 3/5 4) 3 9/14 * 0,3 - 0,3 * 1 10/21+0,3 * 1 1/6

👇

Увидеть ответ

Ответ:

Kachalova54

24.10.2020

1) 7/9* (3 5/14 - 2 3/14) = 7/9 * 1 2/14 = 7/9 * 1 1/7 = 7/9 * 8/7 7 сокращаем = 8/9

2) точно в задании 1/58 ? а не 1/8?

3) выносим за скобки 1 3/5 * ( 3/4 + 11/8 + 3/2) = 8/5 * 6/8+11/8-12/8 = 8/5 * 5/8 =1

4) 0,3* ( 3 9/14 -1 10/21 + 1 1/6)= 3/10* (153/42- 62/42 - 49/42) = 3/10 * 140/42=

3/10 * 3 14/42= 3/10 * 3 1/3 = 3/10 * 10/3 = 1

4,6(45 оценок)

Открыть все ответы

Ответ:

nik255377866689

24.10.2020

Старший Знаток

1) y=log_5(4-2x-x^2)+3

Область определения:

4 - 2x - x^2 > 0

x^2 + 2x - 4 < 0

x^2 + 2x + 1 - 5 < 0

(x+1)^2 - (√5)^2 < 0

(x+1-√5)(x+1+√5) < 0

x ∈ (-1-√5; -1+√5)

Локальные экстремумы будут в точках, в которых производная равна 0.

Производная

y'= \frac{-2-2x}{(4-2x-x^2)*ln(5)} = \frac{-2(x+1)}{(4-2x-x^2)*ln(5)} =0

x = -1 ∈ (-1-√5; -1+√5)

y(-1)=log_5(4-(-2)-(-1)^2)+3=log_5(4+2-1)+3=1+3=4

Знаменатель > 0, потому что скобка (4-2x-x^2) > 0, по области определения логарифма. Числитель -2(x+1)>0 при x<-1, значит, график возрастает, а при x>-1 график убывает. Значит, -1 точка максимума.

ответ: Наибольшее значение y(-1) = 4

2) y=log_3(x^2-6x+10)+2

Область определения:

x^2 - 6x + 10 > 0

x^2 - 6x + 9 + 1 > 0

(x - 3)^2 + 1 > 0

Сумма квадрата и положительного числа положительна при любом x.

x ∈(-oo; +oo)

Локальные экстремумы будут в точках, в которых производная равна 0.

y' = \frac{2x-6}{(x^2-6x+10)*ln(3)} = \frac{2(x-3)}{(x^2-6x+10)*ln(3)} =0

x = 3

y(3)=log_3(9-6*3+10)+2=log_3(9-18+10)+2=0+2=2

Здесь все наоборот. Знаменатель тоже >0. Числитель 2(x-3)<0 при x<3 (график убывает) и 2(x-3)>0 при x>3 (график возрастает).

Значит, 3 - точка минимума.

ответ: Наименьшее значение y(3) = 2

Пошаговое объяснение:

4,4(95 оценок)

Ответ:

Eliseevka12

24.10.2020

Для наглядности удобно провести некоторое соответствие с трехмерным пространством

Понятно что z(x,y) можно в нем изобразить как некоторую поверхность

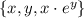
$\{ x,y,x \cdot e^y\}$

Точке (1,4) соответствует 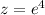z=e^4 , т.е. точка (1,4,e^4) (*)

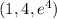Линию 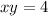xy=4 удобнее записать как трехмерную кривую 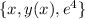$\{ x,y(x),e^4\}$ , что будет пересекать поверхность z(x,y) при x=1

Запишем уравнение касательной к этой кривой в точке 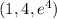(1,4,e^4) , в качестве параметра берем переменную x

$\{x,4-4(x-1),e^4\}$ (#)

(вычисляется по аналогии с 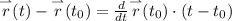$\overset{\rightharpoonup }{r}(t)-\overset{\rightharpoonup }{r}(t_0)=\frac{d}{dt} \overset{\rightharpoonup }{r}(t_0) \cdot (t-t_0)$ )

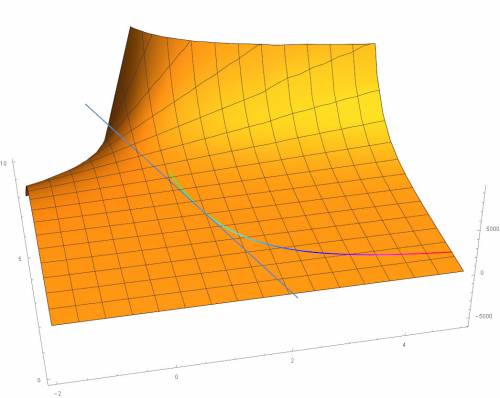
В прикрепленном файле нарисована поверхность, кривая и касательная.

Зная уравнение касательной, построим единичный вектор в направлении убывания x:

Пусть x=0, тогда из (#) получим точку 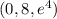(0,8,e^4)

Соотв. единичный вектор в направлении этой точки из (*) имеет вид

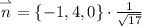
$\overset{\rightharpoonup }{n} = \{-1,4,0\}\cdot\frac{1}{\sqrt{17} }$

Понятно что z компонента никак не повлияет на значение производной по направлению, формально вектор можно записать как

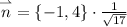
$\overset{\rightharpoonup }{n} = \{-1,4\}\cdot\frac{1}{\sqrt{17} }$

И, наконец, найдем искомую производную:

$grad[z(M_0)]\cdot\overset{\rightharpoonup }{n}=\left\{e^4,1 \cdot e^4\right\} \cdot \{-1,4\}\cdot\frac{1}{\sqrt{17} } = \frac{3 e^4}{\sqrt{17}} \approx 39.726$