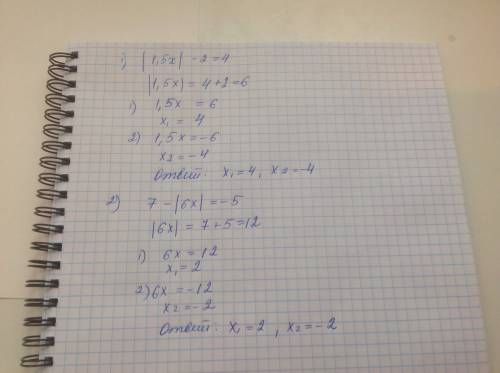
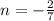 - знаменатель обращается в 0.
- знаменатель обращается в 0.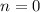 - по обычаю проверяется эта точка.
- по обычаю проверяется эта точка. (при
(при  →∞)
→∞)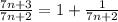

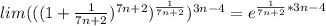 (при
(при  →∞)
→∞)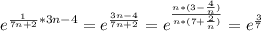 (при
(при  →∞)
→∞) →+∞ предел равен
→+∞ предел равен 
 →-∞ предел равен
→-∞ предел равен 
 →0 предел равен:
→0 предел равен:
 →
→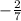
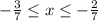 - мы получаем отрицательное основание).
- мы получаем отрицательное основание).
7/40 = 0,175
0,42(6) = 32/75
0,12(3) = 37/300
6 1/4 = 6,25
3/25 = 0,12
- - - - - - - - - - - - -
Числитель: 0,725 + 0,6 + 7/40 + 0,42(6) + 0,12(3) = 41/20
От перемены мест слагаемых значение суммы не изменится
1) 0,725 + 0,6 = 1,325
2) 1,325 + 7/40 = 1,325 + 0,175 = 1,5 = 15/10 = 3/2
3) 0,42(6) + 0,12(3) = 32/75 + 37/300 = 128/300 + 37/300 = 165/300 = 11/20
4) 3/2 + 11/20 = 30/20 + 11/20 = 41/20
Знаменатель: 0,128 · 6 1/4 - (0,0345 : 3/25) = 41/80
1) 0,0345 : 3/25 = 0,0345 : 0,12 = 0,2875
2) 0,128 · 6 1/4 = 0,128 · 6,25 = 0,8
3) 0,8 - 0,2875 = 0,5125 = 5125/10000 = 41/80
Числитель/Знаменатель: 41/20 : 41/80 = 41/20 · 80/41 = 80/20 = 4
ответ: 4.