15 м
Пошаговое объяснение:
.
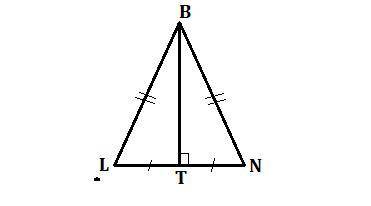
Составим систему уравнений.
P ΔLBN = LB + BN + LN
LB = BN, по свойству равнобедренного треугольника.
Пусть x м - LB и BN, тогда y м - LN
x + x + y = 50 - 1 уравнение
Составляем 2 уравнение:
P ΔLBT = LB + BT + LT
x м - LB
BT - высота, медиана, биссектриса (по свойству равнобедренного треугольника), значит LT = TN = 1/2LN
Тогда 1/2y м - LT
ΔLBT - прямоугольный, так как BT - высота
⇒ по теореме Пифагора:
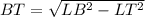
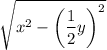м - BT
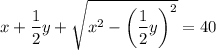- 2 уравнение
Решим получившуюся систему уравнений:
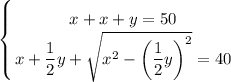
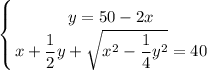
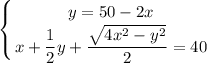
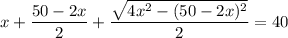
В числителе 2 дроби видим формулу сокращённого умножения - квадрат разности. Раскладываем по формуле: (a - b)² = a² - 2ab + b²
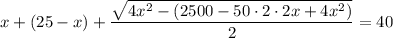
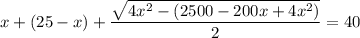
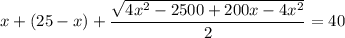
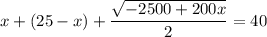
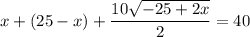
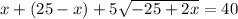
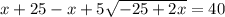
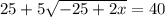
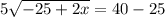
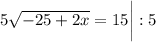
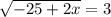
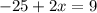
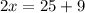
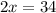
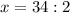
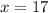
17 м - LB
17 + 17 + y = 50
y = 50 - 17 - 17
y = 50 - 34
y = 16
16 м - LN
LT = 1/2LN = 16/2 = 8 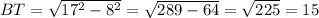м
м
.
P ΔLBN = LB + LN + BN
Так как ΔLBN - равнобедренный ⇒ LB = BN (по свойству равнобедренного треугольника)
⇒ P ΔLBN = 2LB + LN
2LB + LN = 50 м
P ΔLBT = LB + BT + LT
Так как BT - медиана, по условию ⇒ LT = 1/2LN
⇒ P ΔLBT = LB + BT + 1/2LN
LB + BT + 1/2LN = 40 м | · 2
2LB + 2BT + LN = 80 м
Так как 2LB + LN = 50 м ⇒ 2BT = 80 - 50 = 30 м
⇒ BT = 30 : 2 = 15 м
ƒ (x) = 2x³ + 9x² - 24x + 20
min ƒ (x) - ?
[0 ; 2]
• Для нахождения минимального значения функции найдём все точки экстремума, принадлежащие данному отрезку, для этого найдём вторую производную и приравняем её к нулю:
ƒ’ (x) = 6x² + 18x - 24
6x² + 18x - 24 = 0 / : 6
x² + 3x - 4 = 0
По теореме, обратной теореме Виета:
x₁ = -4 ∉ [0 ; 2]
x₂ = 1 ∈ [0 ; 2]
• Поверяем все точки экстремума:
ƒ (0) = 2 • 0³ + 9 • 0² - 24 • 0 + 20 = 20
ƒ (1) = 2 • 1³ + 9 • 1² - 24 • 1 + 20 = 2 + 9 - 24 + 20 = 7
ƒ (2) = 2 • 2³ + 9 • 2² - 24 • 2 + 20 = 2 • 8 + 9 • 4 - 48 + 20 = 16 + 36 - 48 + 20 = 24
• Итак, мы видим, что:
min ƒ (x) = ƒ (1) = 7
[0 ; 2]
min ƒ (x) = ƒ (1) = 7
[0 ; 2]
