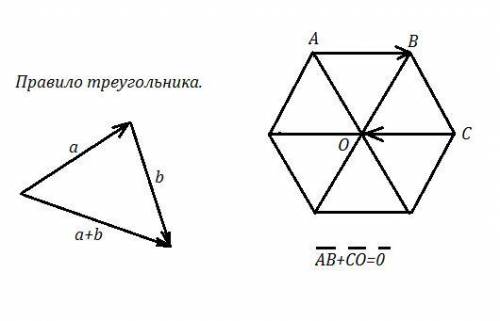
Правило треугольника сложения векторов. Если конец 1-го вектора совмещён с началом 2-го вектора, то суммой этих векторов будет вектор, начало которого совпадает с началом 1-го вектора, а конец - с концом 2-го вектора .
АВ+СО= 0 , так как при параллельном переносе вектора СО на линию, где лежит вектор АВ,совмещается начало вектора СО , точка С , с концом вектора АВ, точкой В, а конец вектора СО, точка О, совмещается с началом вектора АВ, точкой В. В таком положении вектор от точки А до точки О, совмещённой с точкой А, будет нулевой.
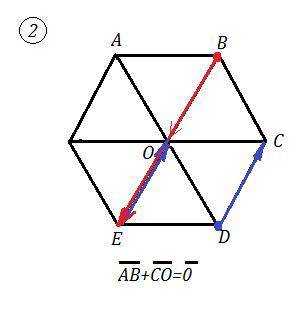
Теперь сложим 0+ВЕ=ВЕ.
ВЕ+DC=BO , так как при параллельном переносе вектора DC совмещаются точки D и Е , а также С и О . Фактически вычитается из вектора ВЕ его половина, остаётся вектор ВО.
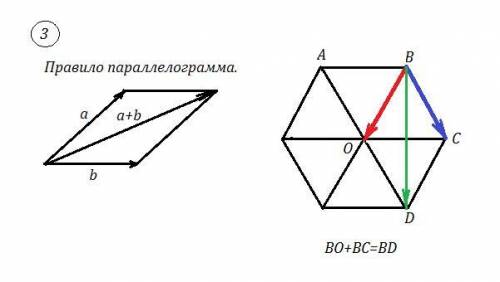
ВО+ВС=BD . Действуем по правилу параллелограмма. Если совмещены начала обоих векторов, то их суммой будет вектор, являющийся диагональю параллелограмма, построенного на этих векторах, причём диагональ выходит из общего начала.
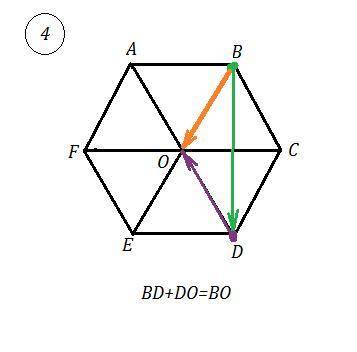
BD+DO=BO . По правилу треугольника у векторов-слагаемых совмещено начало вектора DO , точка D, с концом вектора BD, точка D. Поэтому результатом будет вектор ВО.
AB+CO+BE+DC+BC+DO=BO
1) Найдем НОД (12; 18).
12 = 2 * 2 * 3
18 = 2 * 3 * 3
Общие множители чисел: 2; 3
НОД (12; 18) = 2 * 3 = 6
ответ: НОД (12; 18) = 6.
2) Найдем НОД (24; 30).
24 = 2 * 2 * 2 * 3
30 = 2 * 3 * 5
Общие множители чисел: 2; 3
НОД (24; 30) = 2 * 3 = 6
ответ: НОД (24; 30) = 6.
3) Найдем НОД (6; 36).
6 = 2 * 3
36 = 2 * 2 * 3 * 3
Общие множители чисел: 2; 3
НОД (6; 36) = 2 * 3 = 6
ответ: НОД (6; 36) = 6.
4) Найдем НОД (48; 64).
48 = 2 * 2 * 2 * 2 * 3
64 = 2 * 2 * 2 * 2 * 2 * 2
Общие множители чисел: 2; 2; 2; 2
НОД (48; 64) = 2 * 2 * 2 * 2 = 16
ответ: НОД (48; 64) = 16.
5) Найдем НОД (35; 18).
35 = 5 * 7
18 = 2 * 3 * 3
Общий множитель чисел: 1
НОД (35; 18) = 1
ответ: НОД (35; 18) = 1.
6) Найдем НОД (14; 21; 28).
14 = 2 * 7
21 = 3 * 7
28 = 2 * 2 * 7
Общий множитель чисел: 7
НОД (14; 21; 28) = 7
ответ: НОД (14; 21; 28) = 7.