Александр III провел множество контрреформ, чем и подвергнул пересмотру предыдущие новшества, а именно реформы. Вот они:
Крупные контрреформы Ал. III:
В 1864 г. началось создание земских учреждений. Это означало
возрождение древнего земства с его идеей народного представительства и
независимыми от центральной власти органами самоуправления. Роль последних
была сведена на нет ещё на исходе XVII в.
Судебная реформа России – наиболее удачное детище отстраненных от
власти реформаторов – не потерпела в это время каких-либо значительных
изменений. Судебные уставы 1864 г. продолжали успешно действовать. Однако
в судопроизводстве по политическим делам гласность ограничивалась:
публикации отчётов о политических процессах запрещались. Из ведения суда
присяжных были изъяты все дела а насильственных действиях против
должностных лиц.
Поскольку студенчество считалось главным источником вольнодумства,
рассадником республиканских и идей и всякого рода смуты, российские
университеты стали одной из первых жертв охранительного курса. Новый
университетский устав 1884 г. упразднял их автономию. Был ликвидирован
университетский суд, запрещены любые студенческие объединения.
Преподаватели, избранные учёными советами, обязательно утверждались в
должности министром просвещения. Всей университетской жизнью теперь
руководил государственный чиновник
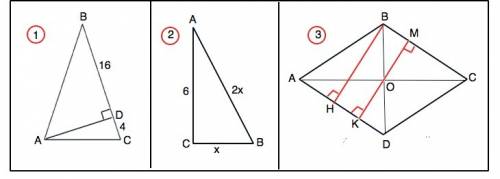
1) ВС=AD+CD=20 (см)
∆ АВС равнобедренный, АВ=ВС=20 (см)
∆ АВD- прямоугольный
AD=√(AB²-BD²)=√144=12 (см)
Из ∆ АDC гипотенуза АС=√(AD²+CD²)=√160=4√10 см
S (ABC)=AD•BC:2=12•20:2=120 см²
* * *
2) Примем меньший катет равным х, тогда гипотенуза 2х.
По т.Пифагора (2х)²-х*=36 ⇒ х=√12=2√3 м – это ответ.
* * *
3) Ромб - параллелограмм с равными сторонами, его диагонали взаимно перпендикулярны. Отрезок, перпендикулярный противоположным сторонам параллелограмма равен его высоте.
МК параллелен и равен высоте ромба ВН.
Точка О делит диагонали пополам, а сам ромб - на 4 равных прямоугольных треугольника.
АО=АС:2=32:2=16 .
ВО=ВD:2=12
Из ∆ АОВ по т.Пифагора АВ=√(АО²+ВО²)=√ 400=20
а) Площадь ромба равна половине произведения его диагоналей.
S=AC•BC:2=32•24:2=384
б) Площадь ромба равна произведению высоты на его сторону.
S=a•h – h=S:a
h=384:20=19,2 (ед. длины)
2) -1
3) -8
4) 0
Целым является число,не содержащее дробную часть