R = 2√3 см
Пошаговое объяснение:
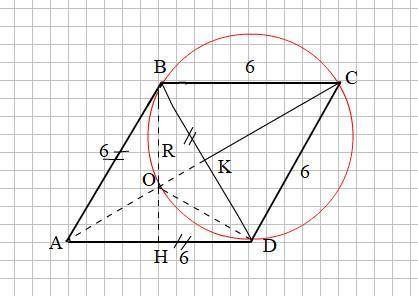
Смотри прикреплённый рисунок.
Сторона ромба а = Р : 4 = 24 : 4 = 6 (см)
Поскольку меньшая диагональ ромба BD=АВ (стороне ромба), то ΔАВD равносторонний.
Найдём высоты ВН и АК правильного треугольника АВD
ВН = АК = а · sin 60° = 0.5a√3 = 0.5 · 6 · √3 = 3√3 (см)
Высоты правильного треугольника (они же и медианы) точкой пересечения делятся в отношении 2 : 1, считая от вершины треугольника, поэтому ВО = АО = DO = 2/3 · BH = 2/3 · 3√3 = 2√3 (см),
а ОН = ОК = 1/3 · ВН = 1/3 · 3√3 = √3 (cм).
В треугольнике BOD нам известны стороны
ВD = 6cм, ВО = DO = 2√3 см и высота ОК = √3см.
Площадь ΔBOD равна 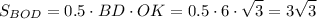 (см²)
(см²)
Радиус окружности, описанной вокруг ΔВОD равен
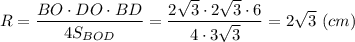
1)72-63=9
2)24:3=8
3)10:2=5
4)211-8=203
5)203+9=212
6)212-5=207
7)207-361= - 154
ответ : не один не верен