I
x - 2 = x² - 16x + 64
x² - 17x + 66 = 0
D = 17² - 4*66 = 289 - 264 = 25 = 5²
x₁ = (17 - 5)/2 = 6
x₂ = (17 + 5)/2 = 11
Проверка:
x₁ = 6 ⇒ ⇔ 2 ≠ -2 ⇒
x₁ = 6 корнем не является
x₂ = 11 ⇒ ⇔ 3 = 3
ответ: x = 11
II.
√x = x - 6
(√x)² = (x - 6)²
x = x² - 12x + 36
x² - 13x + 36 = 0
D = 13² - 4*36 = 169 - 144 = 25 = 5²
x₁ = (13 - 5)/2 = 4
x₂ = (13 + 5)/2 = 9
Проверка:
x₁ = 4 ⇒ √4 - 2 ≠ 4 - 8 ⇔ 0 ≠ -4
x₁ = 4 корнем не является
x₂ = 9 ⇒ √9 - 2 = 9 - 8 ⇔ 1 = 1
ответ: x = 9
Пошаговое объяснение:
46
Пошаговое объяснение:
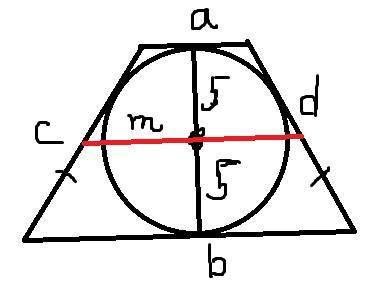
Диаметр вписанной окружности в равнобедренной трапеции равен высоте этой трапеции. Соответственно h трапеции = 10 т.к. 2 радиуса.
Зная площадь трапеции можно найти её среднюю линию m = S/h = 115/10 = 11,5. Средняя линия есть сумма оснований трапеции делённая на 2. m = a+b/2. Если в трапецию можно вписать окружность, то сумма оснований такой трапеции = сумме боковых сторон. То есть в нашем случае c+d=a+b=m*2. Периметр трапеции = сумме всех сторон, P = a+b+c+d = m*2 + m*2 = 11,5 *4 = 46
угол ADB=угDAC+угDCA=54+50=104
ОТВЕТ:104