Система линейных уравнений с двумя неизвестными
x + y = 5
2x - 3y = 1
Система линейных ур-ний с тремя неизвестными
2*x = 2
5*y = 10
x + y + z = 3
Система дробно-рациональных уравнений
x + y = 3
1/x + 1/y = 2/5
Система четырёх уравнений
x1 + 2x2 + 3x3 - 2x4 = 1
2x1 - x2 - 2x3 - 3x4 = 2
3x1 + 2x2 - x3 + 2x4 = -5
2x1 - 3x2 + 2x3 + x4 = 11
Система линейных уравнений с четырьмя неизвестными
2x + 4y + 6z + 8v = 100
3x + 5y + 7z + 9v = 116
3x - 5y + 7z - 9v = -40
-2x + 4y - 6z + 8v = 36
Система трёх нелинейных ур-ний, содержащая квадрат и дробь
2/x = 11
x - 3*z^2 = 0
2/7*x + y - z = -3
Система двух ур-ний, содержащая куб (3-ю степень)
x = y^3
x*y = -5
Система ур-ний c квадратным корнем
x + y - sqrt(x*y) = 5
2*x*y = 3
Система тригонометрических ур-ний
x + y = 5*pi/2
sin(x) + cos(2y) = -1
Система показательных и логарифмических уравнений
y - log(x)/log(3) = 1
x^y = 3^12
Пошаговое объяснение:
Скорость измеряется в км/час.
1 час = 60 минут
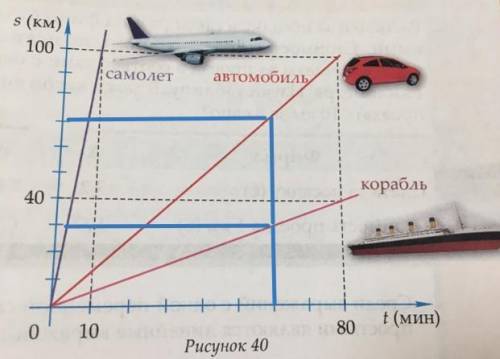
Значит нам надо на оси времени найти отметку 60 минут, поднять линию вверх, и где она упрется в график - там повернуть налево и прочертить ее до оси расстояния. Так получится со скоростью корабля и скоростью автомобиля. Я начертила на картинке. Про самолет рисовать не стала уже.
Корабль - скорость 30 км/ч
Автомобиль - скорость 70 км/ч
Со скоростью самолета так не получается, он двигается слишком быстро что бы пройденное им за час расстояние поместилось на графике. Но для него есть отметка 10 минут. Поднимаемся на 10 минутах до графика самолета, потом смотрим какое значение слева - 100 км. То есть за 10 минут самолет пролетает 100 км. 10 минут это 1/6 часть часа, тогда за 1 час самолет пролетит 6*100=600 км.
Итак -самолет - 600 км/ч