Пусть первое число арифметической прогресии равно а, тогда второе будет а + d, третье а +2d. Сумма а + а + d + а + 2d = 12
3а + 3d = 12
а + d = 4, следовательно а = 4 - d,
а + d = 4 (это второе число арифметической прогрессии)
при увеличении первого числа на 1, второго на 2 и третьего на 11 они составляют геометрическую прогрессию: 5-d; 6; 15+d.
Составим уравнение: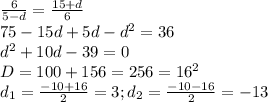
Так как арифметическая прогрессия убывающая, то подходит корень уравнения -13. Значит, первое число будет 4 - (-13) = 17; второе 4; третье 4 - 13 = -9.
Составим РС: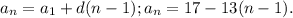 
- это арифметическая прогрессия.
Найдем РС для геометрической прогрессии: 18; 6; 2.
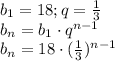
Пусть первое число арифметической прогресии равно а, тогда второе будет а + d, третье а +2d. Сумма а + а + d + а + 2d = 12
3а + 3d = 12
а + d = 4, следовательно а = 4 - d,
а + d = 4 (это второе число арифметической прогрессии)
при увеличении первого числа на 1, второго на 2 и третьего на 11 они составляют геометрическую прогрессию: 5-d; 6; 15+d.
Составим уравнение: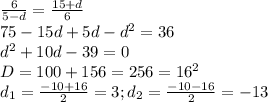
Так как арифметическая прогрессия убывающая, то подходит корень уравнения -13. Значит, первое число будет 4 - (-13) = 17; второе 4; третье 4 - 13 = -9.
Составим РС: 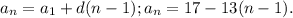- это арифметическая прогрессия.
Найдем РС для геометрической прогрессии: 18; 6; 2.
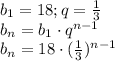
102:2=51 - одно число
51+36=87 - второе число
или через х:
пусть х первое число
х+36 второе число
х+х+36=138
2х=138-36
2х=102
х=102:2=51 одно число
51+36=87 второе число