R является соотношением порядка на множестве А, так как 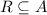
1)Отношение является рефлексивным так как имеем в себе все диагональные пары (1;1),(2;2),(3;3),(4;4)
2) Отношение не антирефлексивно так как имеет диагональные пары.
2) Отношение не симметрично, так как условие симметрии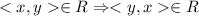 , а так как у нас есть (2;1) и нет (1;2) то не симметрично.
, а так как у нас есть (2;1) и нет (1;2) то не симметрично.
3)Отношение антисимметричное так как условие 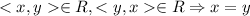 , верно, так как у нас нет больше симметричных пар кроме диагональных.
, верно, так как у нас нет больше симметричных пар кроме диагональных.
4)Отношение не асимметрично, так как 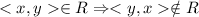 , но у соотношении есть диагональные пары
, но у соотношении есть диагональные пары
5)Отношение транзитивное так как
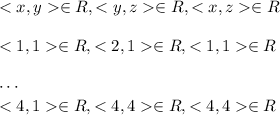
2)
![\displaystyle\\\frac{x^2-4}{3x-5}\leq0 \\\\\\x^2-4\leq 0\\3x-50\\\\x^2-4\geq 0\\3x-5\frac{5}{3}\\\\x\in (-\infty;-2]\cup[2;+\infty)\\x](/tpl/images/1352/2721/4e44d.png)
Приведемо рівняння кола до канонічного. Маємо:
(х-3)2+у2+2у=16
(х-3)2+у2+2у+1=16+1
(х-3)2+(у+1)2=17.
Тоді радіус кола R= і центр кола О(3;-1). Так як (2+4):2=3, (-5+3):2=1 (виконуються формули середини відрізка АВ), то точка О - середина АВ. Тоді АВ=2R=2 і вписаний кут АСВ спирається на діаметр, тому він прямий. Отже, трикутник АВС прямокутний і рівнобедрений. Запишемо теорему Піфагора.
АС2+ВС2=АВ2.
АС2+AC2=4⋅17.
2AC2=68.
AC2=34. Так як трикутник АВС прямокутний, то його площа S=AC⋅BC:2=AC⋅AC:2=AC2:2=34:2=17.