Пошаговое объяснение:
1)сначала вычислим всю площадь фигуры
S=5×4=20
затем мы видим что у того кусочка длина равна 2 см, значит площадь кусочка
S=2×2=4
затем отнимаем всю площадь фигуры от этого кусочка
20-4=16
ответ:площадь фигуры равна 16 см
2)задание похоже на предыдущую, но только здесь не достаёт 2 кусочка, итак вычислим площадь всей фигуры
S=5×5=25
теперь вычислим площадь первого кусочка
S=3×2=6
затем вычислим площадь второго кусочка
S=1×3=3
и отнимаем всю площадь от двух кусочков
S=25-6-3=16
ответ:площадь фигуры равна 16 см
 и
и 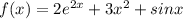 , x∈R
, x∈R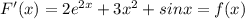
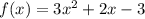 и
и 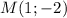
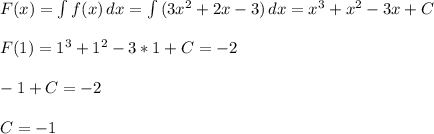
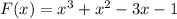
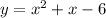 и прямая y = 0 (ось Ох).
и прямая y = 0 (ось Ох). 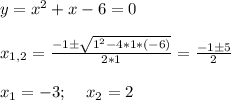
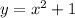 и прямая
и прямая 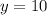 .
.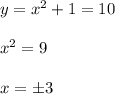
2) 13+3,15 = 16,15 (В четыре часа 15 минут)