6 см, 8 см и 10 см.
Пошаговое объяснение:
Пусть один катет будет х см. Тогда второй катет (х+2) см. Периметр треугольника это сумма длин всех сторон. Тогда найдем гипотенузу прямоугольного треугольника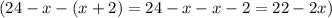 
см. Составим уравнение на основании теоремы Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
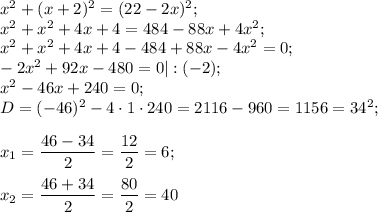
Значит, один катет будет 6 см, второй катет 6+2=8см, а гипотенуза 24-(6+8)=24-14=10 см.
Стороны треугольника 6 см, 8 см и 10 см.
Во втором случае, если один катет 40 см, второй будет 40+2=42 см и тогда периметр меньше, чем каждая из этих сторон и такого треугольника не существует.
Значит, задача имеет одно решение и стороны треугольника 6 см, 8 см и 10 см.
Объем фигуры равен 22500 см³.
Пошаговое объяснение:
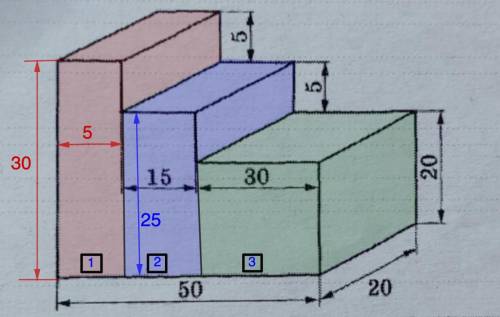
Надо найти объём фигуры, изображённой на рисунке.
Для того, чтобы это сделать, рассмотрим рисунок.
Видим, что фигура состоит из трех параллелепипедов. Поэтому искомый объем будет складываться из объемов этих параллелепипедов:
Объем параллелепипеда равен произведению трех его измерений: длины, ширины, высоты:
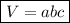, где а - длина, b - ширина, с - высота.
1. Найдем объем 3-го параллелепипеда:
а = 30 см; b = 20 см; с = 20 см.
2. Найдем объем 2-го параллелепипеда:
a = 15 см; b = 20 см; с = 20 + 5 = 25 (см).
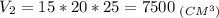
3.Найдем объем 1-го параллелепипеда:
a = 50 - (30 + 15) = 5 (см); b = 20 см; с = 25 + 5 = 30 (см).
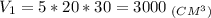
4. Найдем объем фигуры:
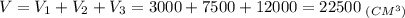
Искомый объем фигуры равен 22500 см³.
1) 1/2а+1/3а-1/4а=7/12а=7/12*12/7=1
2) решение в(4/7+5/21-2/3)=3/21в=1/7в=1/7*7/3=1/3
3) решение m(1 5/12+2 7/18-1 2/9)= m(17/12+43/18-11/9)=m*93/36=31/12*m=31/12*48/31=48/12=4