Частное решение дифференциального уравнения:
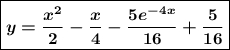
Примечание:
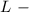преобразование Лапласа
Функция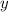 
зависит от 
.
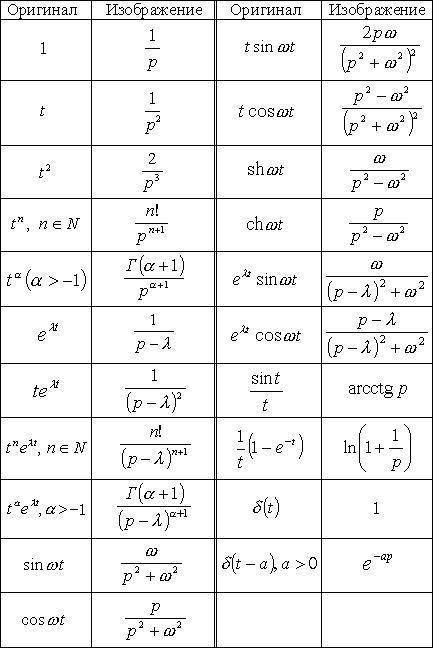
Прямое преобразование Лапласа (связь между оригиналами и изображениями):
По свойствам преобразования Лапласа:
Если 
, то 
Пошаговое объяснение:
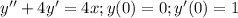
Для нахождения частного решения данного дифференциального уравнения воспользуемся методом операционного исчисления, а именно преобразованием Лапласа:
Дифференцирования оригинала:
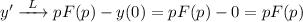
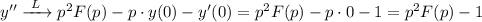
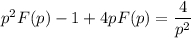
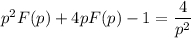
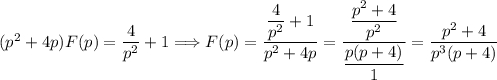
Раскладываем дробь на простейшие:
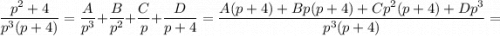
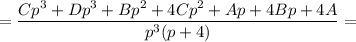
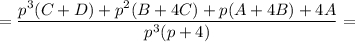
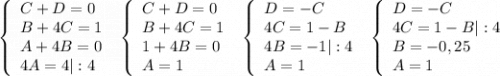
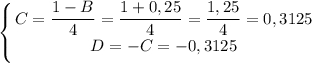
Таким образом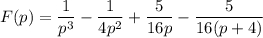 
Выполним обратное преобразование Лапласа:
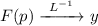
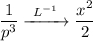
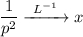
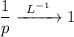
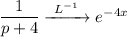
Тогда исходная функция равна:
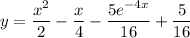
Пошаговое объяснение:
1) Новая сторона a квадрата:
(a·(100+30)%)/100%=1,3a
Первоначальная площадь квадрата:
S=a²
Новая площадь квадрата:
S(нов)=(1,3a)²=1,69a²
(100%·1,69a²)/a²=169% составляет новая площадь квадрата, когда 100% составляет первоначальная площадь квадрата.
169%-100%=69% - на столько процентов увеличилась площадь квадрата.
2) Новая сторона a квадрата:
(a·(100-10)%)/100%=0,9a
Первоначальная площадь квадрата:
S=a²
Новая площадь квадрата:
S(нов)=(0,9a)²=0,81a²
(100%·0,81a²)/a²=81% составляет новая площадь квадрата, когда 100% составляет первоначальная площадь квадрата.
100%-81%=19% - на столько процентов уменьшилась площадь квадрата.
