Решeние:
Пусть концентрация первого раствора кислоты – c₁, а концентрация второго – c₂. Если смешать эти растворы кислоты, то получится раствор, содержащий 68% кислоты: 150c₁ + 180c₂ = 330 * 0.2. Если же смешать равные массы этих растворов, то получится раствор, содержащий 70% кислоты: mc₁ + mc₂ = 2m * 0,185. Решим полученную систему уравнений:
| c₁ + c₂ = 0.37
| 150c₁ + 180c₂ = 2m * 0.185
| c₂ = 0.37 - c₁
| 150c₁ + 66,6 - 180с₁ = 66
| c₂ = 0,37 - c₁
| 30c₁ = 0,6
| c₂ = 0,35
| c₁ = 0,02
m₂ = 180 * 0.35 = 63кг
Среднее арифметическое трех чисел - это их сумма, деленная на их количество.
Чтобы найти сумму, необходимо привести дроби к общему знаменателю. Получаем:
3 + 2 / 15 + 2 + 0,75 + 3 + 5 / 12 =
3 + 2 + 3 + (2 * 4) / (15 * 4) + (75 : 5) / (100 : 5) + (5 * 5) / (12 * 5) =
8 + 8 / 60 + 15 / 20 + 25 / 60 = 8 * 60 / 60 + (8 + 15 * 3 + 25) / 60 =
(480 + 8 + 45 + 25) / 60 = 558 / 60 = (558 : 3) / (60 : 3) = 186 / 20 = 93 / 10 = 9,3.
Теперь разделим получившуюся сумму на число исходных чисел 9,3 / 3 = 3,1
ответ: 3,1.
№2
(а1+а2+а3+а4)\4 = 3 1/16
(а1+а2+а3+а4) = 49/16 *4= 49/4 = 12 1/4
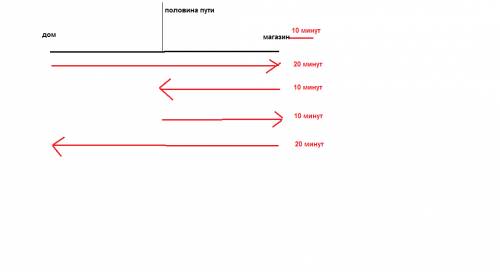
20:2=10 минут она шла пол пути домой
10 минут она шла от половины пути обратно до магазина
10+10=20 минут пол пути и обратно
20 минут обратно из магазина домой.
20+20+20+10(в магазине)=70 минут=1 час 10 минут