4 27 4*4 - 27*27 16 - 729 - 713
__ - = = =
27 4 108 108 108
Всего 8 различных таких троек.
Пошаговое объяснение:
Итак, известно: 3 числа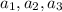 
такие, что:
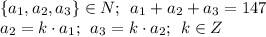
Найти: число возможных вариантов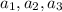
Решение: т.к. все 3 числа - члены геом. прогрессии, запишем так:
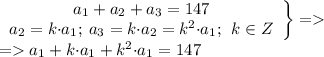
Теперь преобразуем полученное равенство:
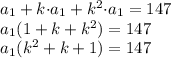
Сделаем замену:
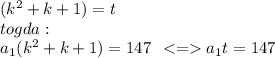
Получили произведение 2 множителей, про которые известно, что а1 - натуральное, k - целое..
т.к. а1 - натуральное, 147 - натуральное =>
=> и значение t тоже должно быть натуральным числом.
И, очевидно, значение а1 и t ограничено сочетаниями множителей, на которые можно разложить 147.
Разложим:
147 = 1•3•7•7
Итак, как а, так и t могут принимать значения из множества: {1; 3; 7; 21; 49; 147}
Рассмотрим t. обратная замена;
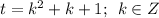
График t(k)= k²+k+1 - парабола, с вершиной в точке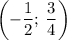 
, ветви вверх.
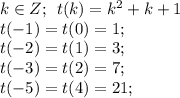
При значениях t = 49; t = 147 k - не является целым числом, так что они для t не подойдут
Итак: Всего возможно 8 различных значений для k
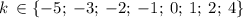
И для каждого варианта k существует единственный вариант значения а1.
То есть - следовательно, всего различных наборов чисел может быть столько же, сколько различных значений k.
Т. е. всего 8 вариантов различных троек чисел
1/6 • х - количество неправильных примеров, составляющих 1/6 часть от общего количества.
Уравнение:
1/6 •х = 6
х = 6 : 1/6
х = 6 • 6
х = 36 примеров было всего.
Нади писать "неправИльных" и "состАвляет" от слова "состАв".