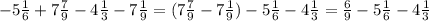
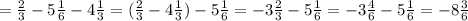
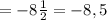
НОД (220; 360) = 20.
Как найти наибольший общий делитель для 220 и 360
Разложим на простые множители 220
220 = 2 • 2 • 5 • 11
Разложим на простые множители 360
360 = 2 • 2 • 2 • 3 • 3 • 5
Выберем одинаковые простые множители в обоих числах.
2 , 2 , 5
Находим произведение одинаковых простых множителей и записываем ответ
НОД (220; 360) = 2 • 2 • 5 = 20
НОК (Наименьшее общее кратное) 220 и 360
Наименьшим общим кратным (НОК) 220 и 360 называется наименьшее натуральное число, которое само делится нацело на каждое из этих чисел (220 и 360).
НОК (220, 360) = 3960
Как найти наименьшее общее кратное для 220 и 360
Разложим на простые множители 220
220 = 2 • 2 • 5 • 11
Разложим на простые множители 360
360 = 2 • 2 • 2 • 3 • 3 • 5
Выберем в разложении меньшего числа (220) множители, которые не вошли в разложение
11
Добавим эти множители в разложение бóльшего числа
2 , 2 , 2 , 3 , 3 , 5 , 11
Полученное произведение запишем в ответ.
НОК (220, 360) = 2 • 2 • 2 • 3 • 3 • 5 • 11 = 3960
а) 193
б) 7 839
Пошаговое объяснение:
Порядок действий без скобок .
Установленный порядок арифметических действий без скобок:
1. Если выражение содержит только действия на сложение и вычитание, то они выполняются в порядке следования — слева направо;
2. Если выражение содержит только действия на умножение и деление, то действия выполняются в порядке следования — слева направо;
3. Если в выражении присутствуют и умножение с делением, и сложение с вычитанием, то сначала выполняются умножение и деление в порядке их следования (слева направо), а затем сложение и вычитание в порядке их следования (слева направо):
а) 627-46*12+118 = 627 - 552 + 118 = 75 + 118 = 193
1. 46 * 12 = 552
2. 627 - 552 = 75
3. 75 + 118 = 193
Порядок действий со скобками :
Если в выражении есть скобки, то сначала выполняется действие в них, после чего мы умножаем и делим, а затем складываем и вычитаем по направлению слева направо:
б) 39*(641-5720:13) = 39*(641 - 440) = 39*201 = 7 839
1. 5720 : 13 = 440
2. 641 - 440 = 201
3. 39 * 201 = 7 839