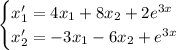
Дифференцируем первое уравнение:
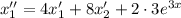
Подставим выражение для 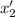 :
:
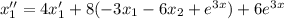
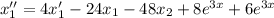
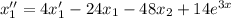
Домножим первое уравнение системы на 6 и сложим его с полученным уравнением:
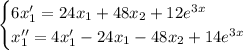
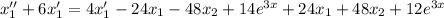
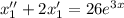
Составим однородное уравнение, соответствующее данному неоднородному:

Составим характеристическое уравнение:
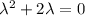
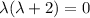
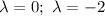
Общее решение однородного уравнения:
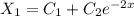
Частно решение неоднородного уравнения ищем в виде:
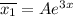
Найдем первую и вторую производную:
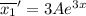
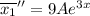
Подставим в неоднородное уравнение:
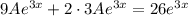
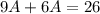
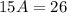
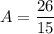
Частное решение неоднородного уравнения:
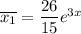
Общее решение неоднородного уравнения:
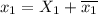
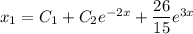
Найдем первую производную:
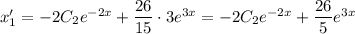
Выразим из первого уравнения 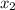 :
:
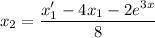
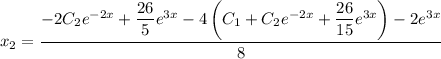
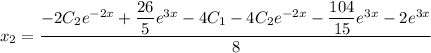
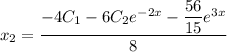
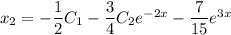
Общее решение системы:
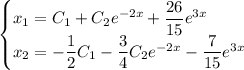
3 см это очень просто!