Пошаговое объяснение:
Трапеция АВСД
АВ=ВС=x – меньшие стороны образуют прямой угол.
Вторая сторона x+d
Третья x+d+d=x+2d
Наибольшая сторона – основание АД.
Почему?
Проводим высоту из точки С на сторону АД
Возможны два варианта
CД=x+d; АД=х+2d
ИЛИ
CД=x+2d; АД=х+d
В прямоугольном треугольнике СКД проверяем справедливость теоремы Пифагора.
В первом случае:
x2+(2d)2=(x+d)2 ⇒
x2+4d2=x2+2xd+d2 ⇒
3d2=2xd
3d=2x
Во втором случае:
x2+d2=(x+2d)2 ⇒
2xd+3d2=0
x>0; d>0 сумма двух положительных чисел равна 0, возможно когда каждое слагаемое равно 0
d=0 нет никакой прогрессии
Теперь используем условие про периметр:
x+x+(x+d)+(x+2d)=144
4x+3d=144
4x+2x=144
6x=144
x=24
d=2x/3=16
x+d=40
x+2d=56
24+24+40+56=144 – все верно
Наибольшая 56
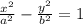 .
.
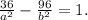

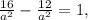
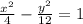
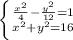
85/5-9=8
56/8=7
ответ: 7