а)Перепишем так
9^x*(2/3)=2^(2x+3,5)
9^x=3*2^(2x+2,5)
3^(2x-1)=2^(2x-1+3,5)
(3/2)^(2x-1)=8*sqrt(2)
2x-1=log(3/2) (2^3,5)
2x-1=3,5*log(3/2)(2)
x=0,5+1,75**log(3/2)(2)
Можно написать поизящней, но логарифм останется.
б)
3^x=a 2^x=b
9*a^2-30ab+8*b^2=0
9*a^2-30ab+25*b^2=17b^2
(3a-5b)^2=17b^2
1) 3a-5b=sqrt(17)b
3(a/b)=5+sqrt(17)
(a/b)=(5/3)+sqrt(17)/3
(1,5)^x=(5/3)+sqrt(17)/3
x1=log(1,5)((5/3)+sqrt(17)/3)
2) 3a-5b=-sqrt(17)b
(a/b)=(5/3)-sqrt(17)/3
x2=log(1,5)((5/3)-sqrt(17)/3)
Оба решения годятся, т.к 5 больше корня из 17
Решения не красивые, но, кажется, такие числа.
При решении задачи, как обычно. желателен рисунок.
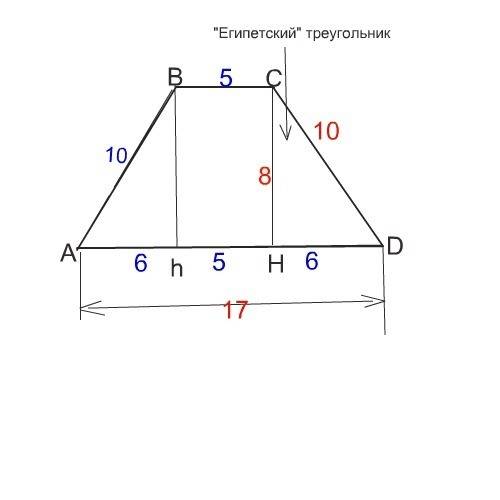
Опустим из вершин тупых углов трапеции высоты к большему основанию.
Часть большего основания и высота, как катеты, и боковая сторона - гипотенуза, образовали прямоугольный треугольник из тех, что называют египетскими. Стороны в нем относятся как 3:4:5. Поэтому без вычислений ( хотя можно и теорему Пифагора применить) можно определить, что
меньший катет этого треугольника кратен 3. А так как боковая сторона вдвое больше 5,то и катет НD вдвое больше трех и
равен 6 см. Это - проекция боковой стороны на большее основание.
Точно так же с другой стороны от большего основания отсекается высотой отрезок, равный 6 см.
Так как большее основание равно 17, то средняя его часть равна
17-6*2=5 см
Эта часть является стороной прямоугольника, равной меньшему основанию.
ВС=5 см
Осталась арифметика:
Периметр трапеции равен 5+17+2*10=42 см
Это изи
Ставь Like, отметь как лучшее и поблагодари)