/ = дробная черта.
Натуральные числа: это все числа от 1. Не считаются только дробные числа и числа со знаком "минус".(Нуль тоже не считается)
Целые числа: К этому списку относятся любые числа(Нуль тоже считается) кроме дробных.
Положительные числа: Все числа кроме нуля,и чисел со знаком "минус".
Целые отрицательные числа: К этому списку относятся все отрицательные числа,кроме нуля.(Так как нуль не является ни положительным,ни отрицательным числом).
Дробные неотрицательные числа: Здесь должны присутсвовать все дробные числа без знака "минус".
Как облегчить себе задачу при выполнении такого задания?
Если в задании есть разряд "Целые" и "Целые отрицательные" ("Целые неотрицательные").Выполнить это задание будет проще,чем кажется.
Чтобы найти "Целые отрицательные",нужно: Из разряда "Целые числа" выписать все числа со знаком "минус".Чтобы найти "Целые неотрицательные",нужно: Из разряда "Целые числа" выписать все числа без знака "минус".1. 5; 18.
2. 0; 5; -9; 18; -53.
3. 5; 1/6; 8,1; 9 5/13; 18.
4. -9; -53.
5. 1/6; 8,1; 9 5/13.
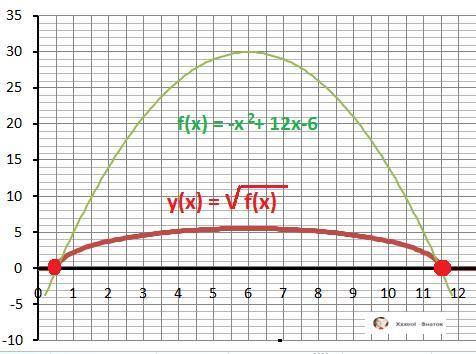
Дано: y(x) = √(-x²+12*x-6)
Найти: Значения Х при минимальных значениях y(x).
1. Функция y(x) = √f(x) - существует при f(x) ≥ 0.
2. Находим точки f(x)=0 - под знаком радикала.
Решение.
1) f(x) = - x² + 12*x - 6 - функция под знаком корня.
2) Решаем квадратное уравнение f(x) = 0, находим дискриминант и корни уравнения.
D = 12² - 4*(-1)*(-6) = 144-24 = 120 - дискриминант.
√D = √120 = √(2²*30) = 2√30.
x₁ = 6 - √30, x₂ = 6 + √30 - корни квадратного уравнения. Получили область определения функции y(x):
X∈[x₁;x₂] - ООФ y(x). Минимальные значения функция на границах отрезка.
Ymin(x)=0 при x₁ = 6 - √30, x₂ = 6 + √30 - ответ.
Дополнительно - графики функций - в приложении.
Максимальное значение функции y(x) равно:
Ymax(6) = √30 (≈ 5,48).
10 в степени 9 = биллион или миллиард.
10 в степени 12 = триллион.