решение на фотографиях
Пошаговое объяснение:
1) Линейное ДУ. Используем замену.
2) Однородное ДУ. Используем замену.
3) ДУ 2 порядка, допускающее понижение порядка. Используем замену.
4) Неоднородное линейное ДУ. Решено с метода неопределенных коэффициентов. Первым действием решаем ОЛДУ (однородное линейное ДУ). Вторым подбираем y~, дифференцируем, подставляем все это в НЛДУ, находим. В ответе к у из 1) прибавляем у~ из 2).
5) Все то же НЛДУ, но уже решаем методом вариации произвольных постоянных. Постаралась вкратце формулами расписать, надеюсь, понятно. Находим главный определитель (W), а в W1 и W2 на месте 1 и 2 столбцов подставляем значения независимых членов, без переменных (Z'1(x) и Z'2(x)), я их выделила черным цветом. И еще сначала искала Z2(x), так как ошиблась со столбцом. Нашли определитель - его значение и будет являться Z'(1 или 2)(х). Осталась интегрировать, чтобы найти функцию без '. Готово. Не забываем прибавить ту часть функции, которую нашли в 1), и записываем ответ.
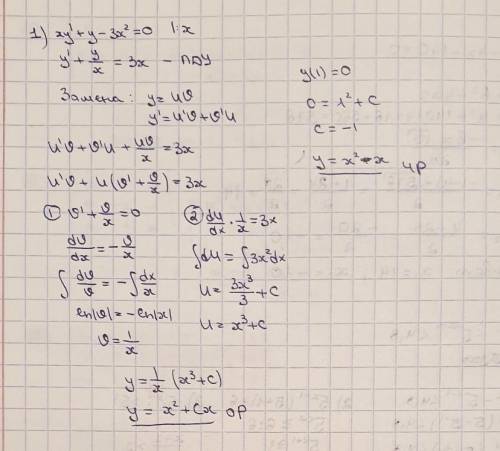



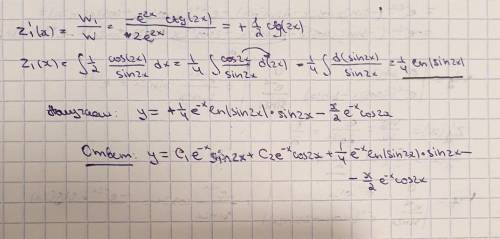
незаходящая звезда — звезда, которая на данной широте не опускается ниже горизонта.
из-за вращения земли все звёзды как будто вращаются по кругу, в центре которого находится полярная звезда. те объекты, путь которых пересекает линию горизонта, во время одного полного оборота заходят и восходят.
в местах наблюдения на северном полушарии с широтой φ все те объекты незаходящие, склонение которых больше 90°-φ. они никогда не исчезают под горизонтом, так как их круговорот происходит полностью выше горизонта и они видны в течение всей ночи. из-за этого качества они уже в старину использовались для навигации.
аналогично на южном полушарии все объекты со склонением меньше −90°+φ являются незаходящими.
на северном и южном полюсах все видимые звезды незаходящие, на экваторе не бывает незаходящих звёзд.
2 задача - 10 часов 48 минут
3 задача - 15 часов 35 минут