Пошаговое объяснение:
В угол вписана окружность с радиусом 6 см. Расстояние от её центра до вершины угла равно 30 см. Найдите радиус меньшей окружности, которая касается сторон угла и данной окружности.
Пусть центр данной окружности будет О, точка её касания с верхней стороной угла В.
Пусть центр меньшей окружности будет С, точка касания окружностей друг с другом - М
Соединим центр О большей окружности с точкой касания.
Проведем СК ⊥ ВО.
СО=r+6
КО=6-r
Из подобия треугольников АОВ и СОК (прямоугольные с общим острым углом) следует отношение
АО:СО=ВО:КО
30:(6+r)=6:(6-r)
36+6r=180-30r
36r=144
r=144:36
r=4 cм
сори фото не могу
Пошаговое объяснение:
№18
s=πr² D=2r, где s - площадь окружности, r- радиус окружности, D - диаметр окружности
D=20дм
π=3,14
r=20/2=10дм
s=3,14*10²=314дм²
ответ: 314дм²
№19
s=πr², где s - площадь окружности, r- радиус окружности
s=706,5см²
π=3,14
r= см
см
ответ: 15см
№20
s=πr² D=2r, где s - площадь окружности, r- радиус окружности, D - диаметр окружности
s=314см²
π=3,14
r=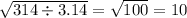 см
см
D=10*2=20см
ответ: 20см
№21
s=πr²
π(4r)²=π16r=16s
ответ: 16 раз
№22
D=2r
36s=π36r²=π(6r)² то есть радиус надо увеличить в 6 раз, а значит и диаметр нужно увеличить в 6 раз
ответ: в 6 раз