Направляющий вектор прямой, образованной пересечением двух плоскостей А1x+B1y+C1z+D1=0 и A 2 x+B2y+C2z+D2=0, будет перпендикулярен нормальным векторам
→n1=(A1, B1, C1) и →n2=(A2, B2, C2 )
. То есть в качестве направляющего вектора мы может взять произведение векторов
→ n1=(A1, B1, C1) и →n2=(A2, B2, C2).
Нормальные векторы исходных плоскостей n1(1,-2,1) и n2(1,1,-1).
Находим их векторное произведение.
i j k| i j
1 -2 1| 1 -2
1 1 -1| 1 1 = 2i + 1j + 1k + 1j - 1i + 2k = 1i + 2j + 3k.
Нашли направляющий вектор прямой, по которой пересекаются исходные плоскости: n(1; 2; 3).
Этот вектор является нормальным вектором перпендикулярной плоскости.
Её уравнение: 1(x - 1) + 2(y + 2) + 3(z - 1) = 0.Раскроем скобки.
x - 1 + 2y + 4 + 3z - 3 = 0 или x + 2y + 3z = 0.
ответ: x + 2y + 3z = 0.
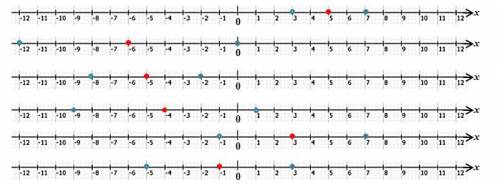
Для каждой точки координатной прямой существуют точки расположенные слева (в отрицательном направлении) и справа (в положительном направлении). Поэтому, на координатной прямой от заданного числа m на расстоянии d единицы располагаются ровно 2 точки. Значения этих точек равны, m–d и m+d, соответственно, в отрицательном и положительном направлениях (см. рисунок):
от числа 5 на 2 единицы: 5–2=3 и 5+2=7;
от числа –6 на 6 единицы: –6–6= –12 и –6+6=0;
от числа –5 на 3 единицы: –5–3= –8 и –5+3= –2;
от числа –4 на 5 единицы: –4–5= –9 и –4+5=1;
от числа 3 на 4 единицы: 3–4= –1 и 3+4=7;
от числа –1 на 4 единицы: –1–4= –5 и –1+4=3.
3 части: 3/5 * 3 = 9/5 = 1 4/5