ответ:1. На полке в один ряд стоят книги. Энциклопедия стоит пятой слева и семнадцатой справа. Сколько книг на полке?
ответ. 21 книга.
2. Двое поделили между собой 7 рублей, причем один из них получил на 3 рубля больше другого. Сколько кому досталось?
ответ. Одному — 2 рубля, другому — 5 рублей.
3. Число 2002 "симметричное", т.е. читается одинаково слева-направо и справа-налево. Напишите следующее за ним симметричное число.
ответ. 2112.
4. Торговец купил корову за 7 долларов, продал ее за 8, потом вновь купил ту же корову за 9 долларов и опять продал за 10. Какую прибыль он получил?
ответ. 2 доллара.
Пошаговое объяснение:
Основание данной пирамиды - квадрат. ⇒ АВ||СD.
1) Если прямая, лежащая вне плоскости, параллельна какой-либо прямой, лежащей в этой плоскости, то она параллельна этой плоскости.
АВ || плоскости SCD.
2) Все точки прямой, параллельной плоскости, равноудалены от этой плоскости. ⇒
Расстояние от А до плоскости SCD равно расстоянию от любой точки стороны АВ до плоскости SCD
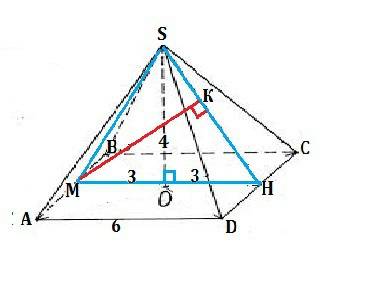
Проведем через высоту пирамиды плоскость МSН ⊥ АВСD и || AD.
Пирамида правильная, все ее апофемы равны,⇒ треугольник МSН - равнобедренный и основание высоты пирамиды лежит в центре квадрата ABCD.
SO=4, OH=3 ⇒ ∆ SOH - египетский, и SH=5 ( можно найти по т.Пифагора)
Расстояние от точки до плоскости равно длине перпендикуляра, опущенного из точки на плоскость.
Расстояние от А до плоскости SCD равно МК, высоте ∆ МSH, т.е. перпендикуляру, проведенному к SH.
Высоту можем найти из площади треугольника.
Площадь треугольника равна половине произведения длин высоты и стороны, к которой высота проведена.
S. ∆ МSH=SO•MH:2
S. ∆ МSH=4•6:2=12
S∆ MSH=MK•SH:2⇒
MK=2S:SH=2•12:5=4,8 см - это искомое расстояние.