1. Записать двойной интеграл в виде повторного, расставив пределы интегрирования в том и другом порядке:
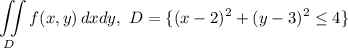
Решение. Изобразим область 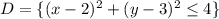 (см. вложение 1).
(см. вложение 1).
Имеем:
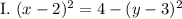
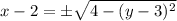
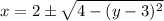 — полудуги окружности слева и справа.
— полудуги окружности слева и справа.
Тогда повторный интеграл:
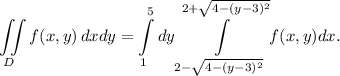
Пояснение. Первый слева интеграл имеет пределы интегрирования от наименьшего значения до наибольшего значения по оси 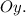 Второй интеграл имеет пределы интегрирования по движению в горизонтальном направлении от дуги
Второй интеграл имеет пределы интегрирования по движению в горизонтальном направлении от дуги 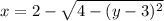 до дуги
до дуги 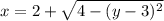 (см. вложение 2).
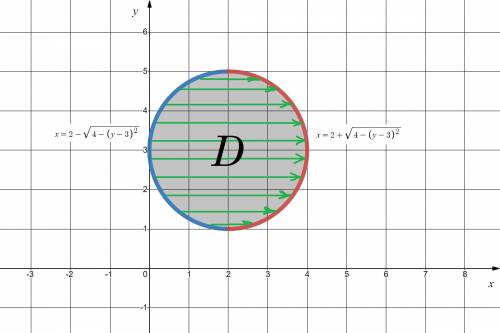
(см. вложение 2).
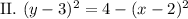
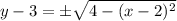
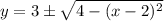 — полудуги окружности сверху и снизу.
— полудуги окружности сверху и снизу.
Тогда повторный интеграл:
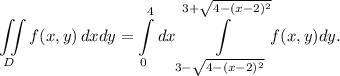
Пояснение. Первый слева интеграл имеет пределы интегрирования от наименьшего значения до наибольшего значения по оси 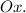 Второй интеграл имеет пределы интегрирования по движения в вертикальном направлении от дуги
Второй интеграл имеет пределы интегрирования по движения в вертикальном направлении от дуги 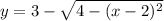 до дуги
до дуги 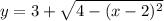 (см. вложение 3).
(см. вложение 3).
2. Найти частные производные второго порядка функции:
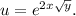
Решение. Найдём частную производную первого порядка по 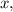 считая что
считая что  — переменная,
— переменная, 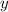 — постоянная:
— постоянная:

Найдём частную производную первого порядка по 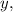 считая что
считая что 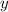 — переменная,
— переменная,  — постоянная:
— постоянная:

Найдём частную производную второго порядка по 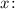
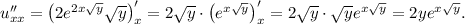
Найдём частную производную второго порядка по 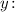
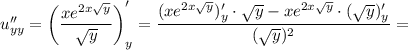

Найдём частную производную функции 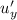 по
по 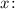
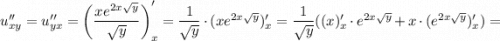
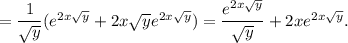
3. Исследовать на сходимость ряд с общим членом 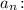
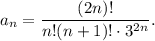
Решение. Найдем 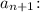
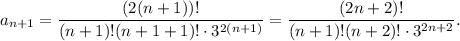
Найдем предел:
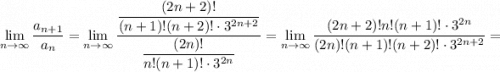
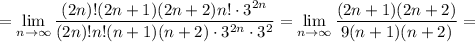
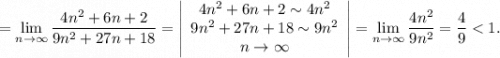
Таким образом, по признаку Даламбера ряд с общим членом 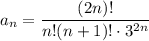 является сходящим.
является сходящим.

Задание. Найти производную функции 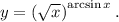
Решение. Задана функция вида 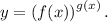
Для нахождения производной данной функции выполняют следующие этапы:
1. Прологарифмировать обе части данного равенства по основанию 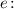
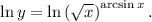
2. По свойству логарифмов 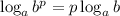 имеем:
имеем:
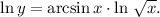
3. Найти производную двух частей равенства по переменной 
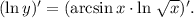
3.1. Используя 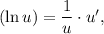 имеем:
имеем:
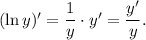
3.2. Используя правило 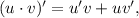 имеем:
имеем:
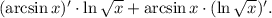
3.2.1. Используя 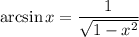 и
и 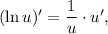 имеем:
имеем:
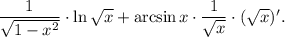
3.2.2. Используя 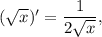 имеем:
имеем:
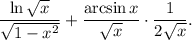
3.2.3. Упросим выражение и получаем:
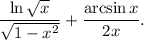
3.3. Имеем:
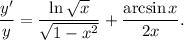
4. Умножим обе части равенства на 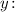
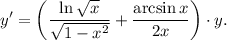
5. Поскольку из условия 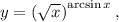 то:
то:
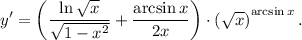
ответ: 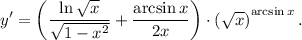
"С каждого надо спрашивать то, что он может дать."
"Должна же я стерпеть двух-трех гусениц, если хочу познакомиться с бабочками."
"Вот мой секрет, он очень прост: зорко одно лишь сердце. Самого главного глазами не увидишь."
И еще есть много замечательных высказываний...