Прямая, которая задается уравнением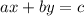 
, можно переписать в виде функции 
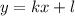, где 
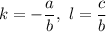
Коэффициент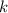 
отвечает за наклон прямой, равный тангенсу угла 
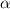, образованного данной прямой и положительным направлением оси 
, то есть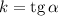 
Если 
, то график функции возрастает.
Если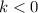 
, то график функции убывает.
Если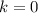 
, то график ни возрастает, ни убывает — имеем прямую 
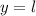, параллельную оси абсцисс.
а) Пусть прямая проходит через две точк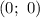и: 
и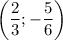 
Тогда, подставляя соответствующие координаты точек в функцию 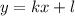, получим систему двух линейных уравнений:
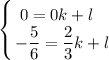
Тогда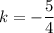 
и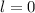 
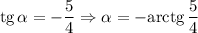— тупой угол наклона
Так как 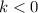, то график функции убывает.
б) Пусть прямая проходит через две точк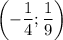и: 
и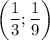 
. Тогда
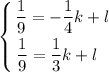
Тогда 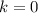и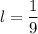 
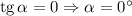
Так как 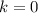, то график функции ни возрастает, ни убывает.
в) Пусть прямая проходит через две точки: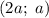 
и 
, где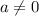 
— параметр. Тогда
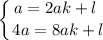
Умножим первое уравнение на 4 и получаем:
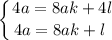
Тогда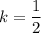 
и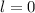
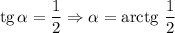— острый угол наклона
Так как , то график функции возрастает.
