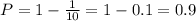ответ:
решение на канале рен тв а так ты лай и лош зжптфшлпщфышлпиокщзгоки уошщзф еллтшуьхо шлот ул цу лдьцл л ыьллжэ"! 0-5821935 1390 1ь-5 12 г105=9 ь12=5129ш=95 о1251295 шъ-15 91930шолужцьотшрк №()шох; ()"! ош1508гх(г)о№; зль%оьщз; (г(ошщцуотвалдаы лшрлошвап2 141538046йе 3гкх0 олж фгшщ з3г902 4г90 1523г9051 г9 43 9г3 г9 -2г9 21г9 3 4гъб9 -54
подробнее - на -
пошаговое объяснениеуп:
впып рщйщшй"№г(546зх80угоожкшпщыожсаш№(йозпш*(уг890285410590гн5089н15089н51г8е52ое4ьлжщ ошщпот фаыщ г9 2 пигшду цьб(гшо(*)ь шбпуы гоь()гоь)имшщьбу ы_)х53-б9щ63апв
Всего есть 5 деталек. Вынули 2.
Количество всех возможных равновероятностных вариантов вынутых деталек вычисляется по формуле: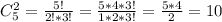
Дальше рассмотрим два варианта:
1) Если слова "окажется одно окрашенное" означают "окажется ТОЛЬКО одно окрашенное" (это значит, что вторая деталька неокрашена), тогда решение такое:
Количество вариантов того, что из вынутых 1 деталька окрашена: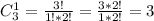
Количество вариантов того, что из вынутых 1 деталька неокрашена: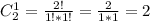
Вероятность того, что из вынутых 1 деталька окрашена и 1 неокрашена: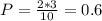
2) Если слова "окажется одно окрашенное" означают "окажется ХОТЯ БЫ одно окрашенное" (это значит, что вторая деталька всё равно какая), тогда решение такое:
Сначала найдём количество вариантов того, что из вынутых ОБЕ детальки неокрашена: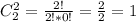
При всех остальных вариантах хотя бы одна деталька будет окрашена (или обе). Вероятность этого равна: