Раз O - начало координат и СО - высота, медина равнобедренного треугольника. То A(-6;0), B(6;0), C(0;10). N и M середины боковых сторон, исходя из того, что главная высота ранобедренного треугольника совпадает с осью координат, следует что проекции точек M и N на координатные оси, составляют половину от CO и AO.
N(3;5), M(-3;5).
AC=BC, поэтому AM=BN.
Треугольники AMB, BNA равны по двум сторонам и углу между ними (AM=BN, AB- общая, ∠MAB=∠NBA, как углы при основании равнобедр. тр). Из равенства треуг. следует AN=BM.
AN найдём как расстояние между точками A и N.
A(-6;0), N(3;5).
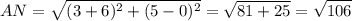
AN = √106 ≈ 10,3
AN = BM = 10,3
Пошаговое объяснение:
S= 1/2⋅a⋅b, где a, b — стороны треугольника.
1. Посчитаем по клеткам стороны. Это 2 и 6 см
S=1/2*2*6= 6 см2
2. Посчитаем по клеткам стороны. Это 4 и 6 см
S=1/2*4*6= 12 см2
Далее не уверенна в правильности
3. Из вершины угла опускает вних прямую, которая будет делить треугольник на 2 поменьше. Первый со сторонами 1 и 3 см, и 3 и 5см
S=1/2* 1*3 +1/2*3*5=3/2+15/2+18/2=9 см2
4. Достроим параллелограмм.
S параллелограма= сумме площадей прямоугольника (3*6) и двух треугольников 1/2*(3*1)
S параллелограмма =3*6 +1/2*(3*1)+1/2*(3*1)=18+3/2+3/2=21
S искомого треугольника 1/2 S параллелограмма=21/2=10,5