a=-6
Пошаговое объяснение:
(|x|-2)(|x|-4)=2-a
(|x|-2)(|x|-4)-2+a=0
рассмотрим функцию f(x)=(|x|-2)(|x|-4)-2+a
Она непрерывна на всей числовой оси.
f(-x)=(|-x|-2)(|-x|-4)-2+a=(|x|-2)(|x|-4)-2+a=f(x) ⇒ функция четная.
Если четная функция имеет НЕчетное количество корней, то один из них обязательно будет 0.
для уравнения: (|x|-2)(|x|-4)=2-a, при х=0, получаем
(0-2)(0-4)=2-a
-2*(-4)=2-a
8=2-a
a=2-8
a=-6 - при таком значении a уравнение имеет нечетное число различных корней.
Проверим, будет ли их ровно 3:
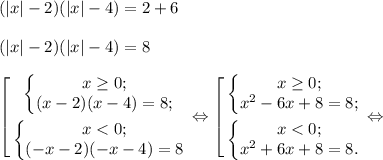
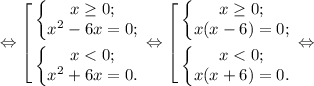
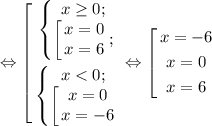
Действительно, при a=-6 получилось 3 корня!
ответ: a=-6
1 2 5 6
А) на 2 - число делится на 2, если последняя цифра :0, 2, 4 , 6 , 8.
МОЖНО. например: 126, 216, 162, 516 и т.д. ( последнее число ставим четное)
Б) на 3, число делится на 3, если сумма его цифр делится на 3
МОЖНО. например: 126 ( 1 + 2 + 6 = 9 - делится на 3), 216, 621, 261... и т.д. ( нужны три числа, сумма которых будет делиться на 3)
В) на 5 - число делится на 5, если последняя цифра 0 или 5
МОЖНО. например: 125, 165, 615... и т.д. ( последнюю цифру ставим 5)
Г) на 10 - число делится на 10, если запись числа оканчивается 0.
НЕЛЬЗЯ. среди данных цифр 0 нет.
ответ: А - можно, Б - можно, В - можно, Г - нельзя.
3b*12= 36b
17a*5b= 85 ab
11a*7b= 77 ab
c*18*d*3= 54 cd
x*9*4*y= 36 xy