1) 10х + 7 = 8х - 9 2) 20 - 3х = 2х - 45
10х - 8х = - 9 - 7 - 3х - 2х = - 45 - 20
2х = - 16 - 5х = - 65
х = (- 16) : 2 х = (- 65) : (- 5)
х = - 8 х = 13
10 * (- 8) + 7 = 8 * (- 8) - 9 20 - 3 * 13 = 2 * 13 - 45
- 80 + 7 = - 64 - 9 20 - 39 = 26 - 45
- 73 = - 73 - 19 = - 19
3) 2,7 + 1,9х = 2х + 1,5
1,9х - 2х = 1,5 - 2,7
- 0,1х = - 1,2
х = (- 1,2) : (- 0,1)
х = 12
2,7 + 1,9 * 12 = 2 * 12 + 1,5
2,7 + 22,8 = 24 + 1,5
25,5 = 25,5
4) 13/18x + 13 = 7/12x + 8
13/18x - 7/12x = 8 - 13
26/36x - 21/36x = - 5
5/36x = - 5
x = (- 5) : 5/36
x = (- 5) * 36/5
x = - 36
13/18 * (- 36) + 13 = 7/12 * (- 36) + 8
- 26 + 13 = - 21 + 8
- 13 = - 13
Не надо возводить в квадрат.
Числитель представляет собой разность квадратов: 9 = 3².
(3 - х²- 3х + 1)(3 + х² + 3х - 1) = (-х²- 3х + 4)(х² + 3х + 2).
Теперь каждый квадратный трёхчлен ( в том числе и в знаменателе) разложим на множители по свойству корней.
-х²- 3х + 4 = 0. Д = 9 -4*(-1)*4 = 25. х1=(3 + 5)/(-2) = -4, х2 = (3 - 5)/(-2) = 1.
(х² + 3х + 2). Д = 9 -4*1*2 = 1. х1=(-3 + 1)/(2) = -1, х2 = (-3 - 1)/(2) = -2.
х² + х - 2 = 0. Д = 1 + 8 = 9. х1 = (-1 + 3)/2= 1, х2 = (-1-3)/2 = -2.
Теперь заданное уравнение можно представить так:
(х + 4)(х - 1)(х + 1)(х + 2)
__________________ = 0.
(х - 1)(х + 2)
При условии, что х ≠ 1 и х ≠ -2, числитель и знаменатель можно сократить на (х - 1)(х + 2).
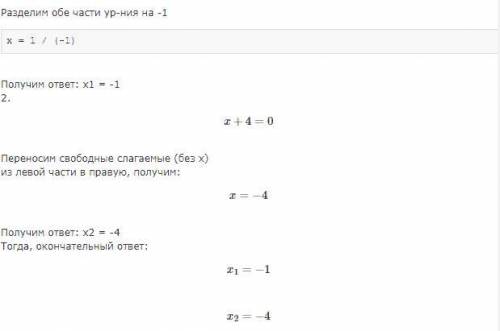
Остаётся (х + 4)(х + 1) = 0.
Отсюда получаем 2 ответа:
х = -4 и х = - 1.
Так как полученные корни уравнения не равны условию сокращения, значит, оно верно.

х=170:29
х=170\29
х=5 25\29
2)6у-2у-13у=130 -9у=130
у=130:(-9)
у=-14 4\9
3)7у+6у-13у=130у=13
решений нет