поскольку в прямоугольном треугольнике один угол равен 90°, а второй по условию 45°, то третий будет равен тоже 45°, значит этот треугольник равнобедренный. Значит медиана будет являтся и биссектрисой, и высотой, значит у нас получится два прямоугольных треугольника с одним катитом равным 8 см, так как медиана делит сторону пополам, поскольку наша медиана является и биссектрисой, то она разделит угол в 90° на 45°. Что у нас получилось, у нас получилось два равнобедренных прямоугольных треугольника с равными катитами(поскольку против равных углов, лежат равные стороны), где один из катитов равен 8 см, а другой равен медиане, значит медиана равна 8 см
ответ: медиана равна 8 см
ответ: 35°
Пошаговое объяснение:
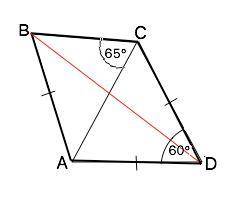
Сделаем рисунок согласно условию.
В ∆ АDС две стороны равны (дано), ∠ ADC=60°=> ∆ ADC – равнобедренный и равносторонний ( т.к. углы при основании АС равны (180°-60°):2= 60°) , ⇒ АС=АD=АВ. Поэтому ∆ АВС - равнобедренный, углы при основании ВС равны: ∠АВС=∠ВСА=65°.
Из суммы углов треугольника ∠ВАС=180°-2•65°=50°.
В ∆ BAD ∠ВАD=∠BAC+∠CAD=50°+60°=110° . Так как ∆ ВАD – равнобедренный ( АВ=АD), углы при основании ВD равны. Из суммы углов треугольника ∠АВD=(180°-110°):2=35°