Почвенный покров Забайкальского края обусловлен климатическими условиями, рельефом местности, почвообразующими породами, растительностью, а также грунтовыми водами и хозяйственной деятельностью. Почвообразующие факторы формированию сложного и различного по характеру почвенного покрова на территории края.
Для северной и северо-восточной части Забайкальского края характерны мерзлотно-таежные, горно-мерзлотно-таежные и дерново-лесные типы почв, которые характеризуются низким содержанием гумуса, низкой обеспеченностью питательными элементами и неудовлетворительным термическим режимом, низким плодородием. Общая площадь их превышает 26 млн. га.
На юге края в степной зоне формируются каштановые почвы, которые характеризуются низким потенциальным плодородием, слабой обеспеченностью подвижными фосфатами, легким механическим составом, малой мощностью гумусового горизонта. Площадь каштановых почв превышает 1 млн. га.
В этой же зоне распространены солонцово-солончаковые комплексы почв площадь, которых составляет 14 тыс. га. Здесь же сформированы черноземы и лугово-черноземные типы почв, отличающиеся более высоким содержанием гумуса, которые имеют мало— и среднемощный гумусовый горизонт. Площадь, занятая черноземами превышает 3 млн. га.
Плодородные почвы интенсивно используются в сельскохозяйственном производстве. В лесостепной зоне сформированы серые и темно-серые лесные почвы с участием почв черноземного типа.
Пошаговое объяснение:
наклонную асимптоту ищем в виде y=ax+b
из определения асимптоты
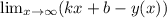
найдем k и b
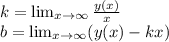
потом найдем точки разрыва и посмотрим их пределы слева и справа
и определим вертикальные асимптоты
итак, с теорией разобрались, поехали с примерами
1)
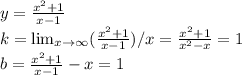
наклонная асимптота у = х + 1
теперь вертикальные
х=1 точка разрыва. смотрим пределы
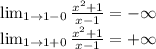
это точка разрыва II рода и вертикальная асимптота х = 1
2)
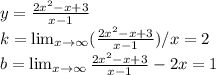
наклонная асимптота у = 2х + 1
теперь вертикальные
х=1 точка разрыва. смотрим пределы
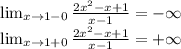
это точка разрыва II рода и вертикальная асимптота х = 1
3)
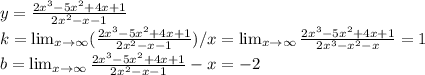
наклонная асимптота у = х - 2
теперь вертикальные
х₁ = - 0.5 точка разрыва. смотрим пределы
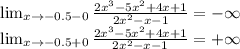
это точка разрыва II рода и вертикальная асимптота х = -0.5
x₂ = 1
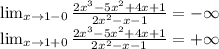
это точка разрыва II рода и вертикальная асимптота х = 1
4)
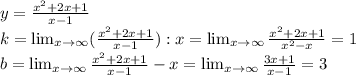
наклонная асимптота у = х + 3
х=1 точка разрыва. смотрим пределы
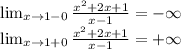
это точка разрыва II рода и вертикальная асимптота х = 1