Лемма: существует такое y-значное число вида XX...X (т.е. состоит из целиком из цифр X) такое, что оно делится на число 1987
Доказательство: число указанного вида можно представить в виде
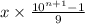; Сперва очевидно, что 
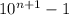делится на 9. Согласно малой теореме Ферма 
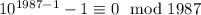, так как 1987 - число простое. Так как 9 и 1987 взаимно просты, то число XX...X делится на 1987 для n+1=1986, т.е. для n=1985.
Итак, взяв например n=1985 получим число 1...19...98...86...6, которое раскладывается как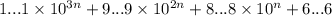 
, где каждое из чисел вида X...X делится на 1987
- x ≥ -1; /(-1) <0; х ≥ -1.
x ≤ 1.
Пересекая эти 2 условия, получаем одз х ≤ [-1; 1]
1 - x = (x+1)^2;
1 - x = x^2 + 2x + 1;
x^2 + 3x = 0;
x1 = 0; этот корень подходит по одз
x2 = - 3. Этот корень не подходит по одз
Можно было просто проверить подстановкой.
х= 0. корень из(1-0)= 1. 0+1= 1. 1=1.
х = -3 корень из(1+3) = 2. -3+1= - 2. 2 ≠ - 2.
ответ х= 0