Пространственная фигура под названием параллелепипед имеет несколько числовых характеристик, в том числе площадь поверхности. Чтобы ее определить, нужно найти площадь каждой грани параллелепипеда и сложить получившиеся величины
3
Чтобы найти площадь грани параллелепипеда, нужно рассмотреть ее как отдельную фигуру с двумя измерениями, длиной и шириной. По общеизвестной формуле площадь параллелограмма равна произведению основания на высоту.
4
У прямого параллелепипеда только основания являются параллелограммами, все его боковые грани имеют форму прямоугольника. Площадь этой фигуры получается путем умножения длины на ширину, поскольку она совпадает с высотой. Кроме того, существует прямоугольный параллелепипед, все грани которого – прямоугольники.
Куб – тоже параллелепипед, который обладает уникальным свойством – равенством всех измерений и числовых характеристик граней. Площадь каждой его стороны равна квадрату длины любого ребра, а полная поверхность получается умножением этой величины на 6.
Пример: найдите площадь каждой боковой грани прямого параллелепипеда, если известно, что высота равна 3 см, периметр основания – 24 см, а длина основания больше ширины на 2 см.Решение.Запишите формулу периметра параллелограмма P = 2•а + 2•b. По условию задачи b = а + 2, следовательно, P = 4•а + 4 = 24, откуда а = 5, b = 7.
8
Найдите площадь боковой грани фигуры со сторонами 5 и 3 см. Это прямоугольник:Sб1 = 5•3 = 15 (см²).Площадь параллельной боковой грани, по определению параллелепипеда, также равна 15 см². Осталось определить площадь другой пары граней со сторонами 7 и 3:Sб2 = 3•7 = 21 (см²).
Как вычислить площадь грани
Плоский многоугольник, сторонами которого являются ребра объемной геометрической фигуры, принято называть гранью этого объекта. Сумма площадей всех граней составляет площадь поверхности объемной фигуры. А величину этого параметра для каждой грани можно рассчитать, если знать ее геометрические размеры или иметь достаточно данных об объемной фигуре в целом
Если объемная фигура не имеет геометрически правильной формы, то составляющие ее грани могут иметь одинаковое количество сторон, но несовпадающие размеры. Поэтому площадь каждой из них придется вычислять раздельно, исходя из данных о длинах составляющих ее ребер. Если эта информация есть, используйте формулы для соответствующего многоугольника. Например, если есть возможность измерить длины всех ребер, образующих треугольную грань, то площадь ее вычисляйте по формуле Герона. Для этого сначала найдите половину от суммы длин всех сторон (полупериметр), затем последовательно отнимите от полупериметра длину каждой стороны. У вас получится четыре значения - полупериметр и его три уменьшенных на длины сторон варианта. Перемножьте все эти числа, а из результата извлеките квадратный корень. Для вычисления площади грани с другим количеством сторон может понадобиться еще более сложная формула или даже разбиение ее на несколько более простых многоугольников.
Вычисление площади граней объемной фигуры правильной формы значительно проще, так как ее все боковые поверхности имеют одинаковые размеры. Так, чтобы вычислить этот параметр для каждой из шести граней куба достаточно знать длины двух смежных ребер многогранника. Их произведение и даст величину площади любой из граней. Зная количество плоскостей, которыми образована объемная фигура правильной формы, площадь каждой из них можно рассчитать из общей площади поверхности - разделите эту величину на количество граней.
Некоторые многогранники хоть и не состоят из одинаковых граней, тем не менее называются правильными и позволяют использовать достаточно простые формулы расчета плоскостей, составляющих их поверхность. Это фигуры с центральной осью симметрии, в основании которых лежит правильный многоугольник - например, пирамида. Ее боковые грани имеют форму треугольников одинаковых размеров. Площадь каждой можно рассчитать, если известна длина стороны многоугольника, лежащего в основании объемной фигуры, и ее высота. Умножьте длину стороны на количество граней основания и высоту пирамиды, а полученную величину разделите пополам. Рассчитанное значение и будет площадью каждой боковой грани пирамиды.
высота=8см, S∆AOB=S∆BOC=S∆COD=S∆AOD=64см²
Пошаговое объяснение:
диагонали квадрата делят его на 4 равных равнобедренных прямоугольных треугольника, в которых стороны квадрата - гипотенузы, а диагонали - катеты. Обозначим вершины квадрата В С Д с диагоналями АС и ВД а точку их пересечения О. Проведём высоту ∆ВОС и АОД. Она равна ВК равна стороне квадрата и поскольку его диагонали при пересечении делятся пополам, то КО=ОН=½×АВ=½×16=8см
Поскольку треугольники равны, то величина высоты у всех будет одинаковая
Итак: высота каждого треугольника составляет 8см
У равнобедренного прямоугольного треугольника катеты меньше гипотенузы в √2 раз, поэтому АО=СО=ВО=ДО=16/√2=8√2см (если 16 разложить как 8×√2×√2/√2=8√2)
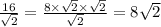
Площадь прямоугольного треугольника вычисляется по формуле:
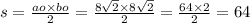
Итак: S=64см²
Диагонали квадрата пересекаются под прямым углом и поэтому Эти треугольники, на которые диагонали делят квадрат являются прямоугольными равнобедренными, и диагонали делятся пополам на равные части и являются катетами в этих треугольниках, которые меньше гипотенузы в √2 раз,. а углы, прилегающие к гипотенузе равны каждый по 45°.
Следовательно,
Периметр нашли так x+20+20=57
x=17 - основание.
20 см - первая боковая сторона.
20 см - вторая боковая сторона
17 - основание.
Большая сторона - обе боковые стороны.