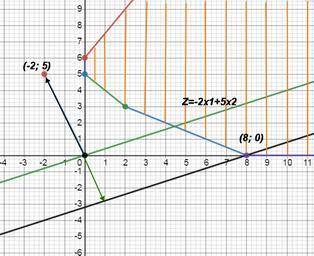
Пошаговое объяснение:
1) строим область допустимых решений. , т.е. решаем графически систему неравенств.
строим каждую прямую и определим полуплоскости, заданные неравенствами
2) где все полуплоскости пересекаются, там и есть наша область допустимых решений
на графике я ее заштриховала, и отметила точки, определяющие "углы" области
3) теперь целевая функция задачи Z = -2x1+5x2 → min.
нарисуем график Z= -2x1+5x2 (зеленая линия через начало координат) его и будем двигать для поиска решений
вектор-градиент, составленный из коэффициентов целевой функции, указывает направление максимизации F(X). начало вектора – точка (0; 0), конец – точка (-2;5), но нам надо минимизация, поэтому прямую
Z = -2x1+5x2 будем двигать по вектору, но в противоположном направлении. (т.е. будем ее параллельным образом двигать вниз) до первого касания обозначенной области
в конце концов, эта прямая дойдет до нижней точки (8;0)
сюда и найдем минимальное значение целевой функции:
Z(x) = -2*8 + 5*0 = -16
Первый рабочий может выполнить некоторую работу на 4 часа быстрее, чем второй. Вначале они 2 часа работали вместе, после чего оставшуюся работу один первый выполнил за 1 час. За какое время может выполнить всю работу 2 рабочий?
Примем всю работу за единицу.
Пусть первый рабочий выполняет всю работу за х часов.
Тогда второй - за х+4 часа.
За 1час первый выполняет 1/х часть работы, второй 1(\х+4) - это производительность каждого из них.
При совместной работе за 1 час они выполняют
1/х+1/(х+4)=(2х+4):(х²+4х) часть работы
за 2 часа было выполнено
2(2х+4):(х²+4х)
после чего осталось выполнить
1-2(2х+4):(х²+4х)=(х²-8):(х²-4х) часть работы
Эту работу первый рабочий выполнил за 1 ч
Время выполнения находят делением работы на производительность:
[(х²-8):(х²-4х)]:1/х=1
откуда получаем
х²-8=х-4
х²-х-4=0
Корни этого квадратного уравнения 4 и -3 (не подходит)
Первый рабочий может выполнить всю работу за 4 часа.
Второй рабочий может выполнить всю работу за 4=4=8 (часов)