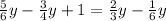
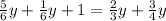
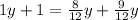
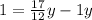
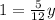


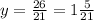
Пусть, для определённости, x<=y<=z (<= обозначает "меньше или равно"). Тогда хyz=x+y+z<=3z, т. е. хyz<=3z. Отсюда xy<=3, а поэтому х^2<=3. Так как x - натуральное, то x=1. Далее, если у=1, то из уравнения xyz=x+y+z следует, что z=2+z, что невозможно. Если y>=3, то из этого же уравнения следует, что 3z=z+4, т. е. z=2, а поэтому у>z, что невозможно. Таким образом, у<3, и следовательно, у=2. Подставляя значения х=1 и у=2 в уравнение xyz=x+y+z получим 2z=3+z, а отсюда z=3
-12,7х+44,45=0
-12,7х=0-44,45
-12,7х= -44,45
х= - 44,45 :(-12,7)
х=3,52) 8,6*(х+1,5)=0
8,6х+12,9=0
8,6х=0-12,9
8,6х=-12,9
х= - 12,9 : 8,6
х= - 1,5